LeetCode 858. Mirror Reflection

每日題。寫起來不是很舒服的題，早上本來看到900個爛，現在已經1300了。倒是沒想到暴力模擬也能過就是了。

題目

有一個特殊的正方形房間，四面牆都是鏡子。除西南角落以外，其他角落都設有接收器，編號0,1,2分別為東南、東北和西北角落。　　 房間的邊長為p，西南角會發射出一道光線，並落在東面牆上距離0號接受器q距離處。

輸入整數p,q並回傳最先接觸到光線的接受器編號，保證每道光一定會碰到接收器。

解法

要採用模擬方式的話，一般來說需要紀錄x,y座標，還需要判斷兩個變數來紀錄一棟方位，才能計算光線下一個抵達位置，光是用想的就很麻煩。

但接收器只會在四個角落，意味著x座標只會在0或是p的時候才有可能是答案。那麼我們可以簡單的只處理x=0或是x=p的情況，若每次光線碰到南北牆面時，直接計算出折射後的落點。

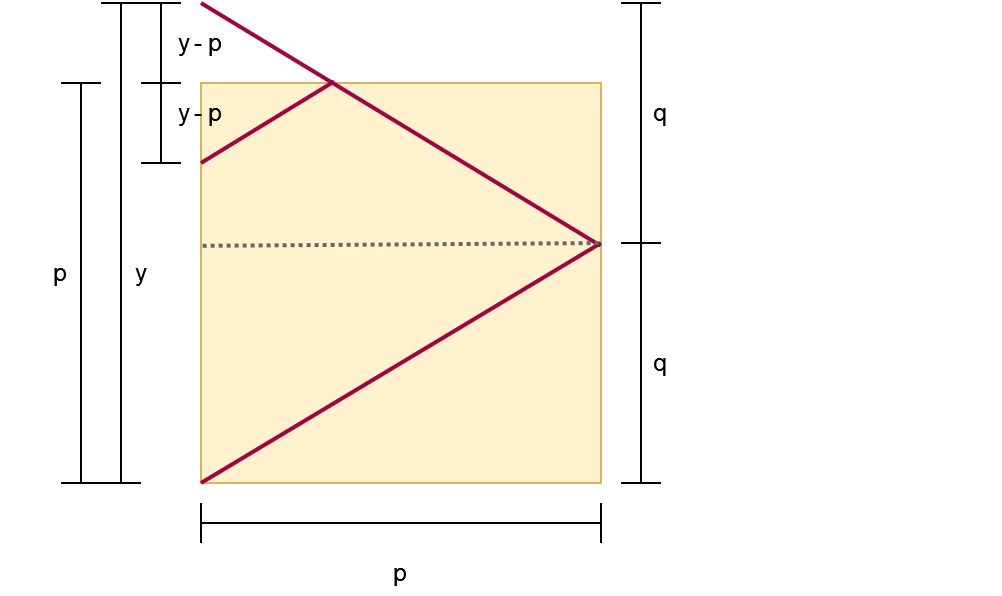
光線每次移動的水平距離為p，所以只要變數left來表示在左右方：在左方時為true，右方為false。
變數y紀錄光線的垂直座標，每次的移動距離應為q，變數up以正負1分別表示上下移動。
每次移動只需要將left變數切換，並將y軸加上對應的移動距離。但在y超過p或是小於0時，代表有部分應折射到相反的垂直方向，這時候應該分別處理：

• 當y大於p時，應從p往下走(y-p)距離
• 當y小於0時，應從0往上(0-y)距離

class Solution:
    def mirrorReflection(self, p: int, q: int) -> int:
        y=0
        left=True
        up=1
        
        while True:
            if left and y==p:return 2
            if not left and y==0:return 0
            if not left and y==p:return 1
            left=not left
            y+=q*up
            if y>p:
                y=p-(y-p)
                up=-up
            elif y<0:
                y=-y
                up=-up

看了其他人的解法，怎麼幾乎都是奇怪的數學解，數學神人這麼多的嗎？
假設光不會反射，而是翻轉房間的相對格局，我也試著畫圖做做看。

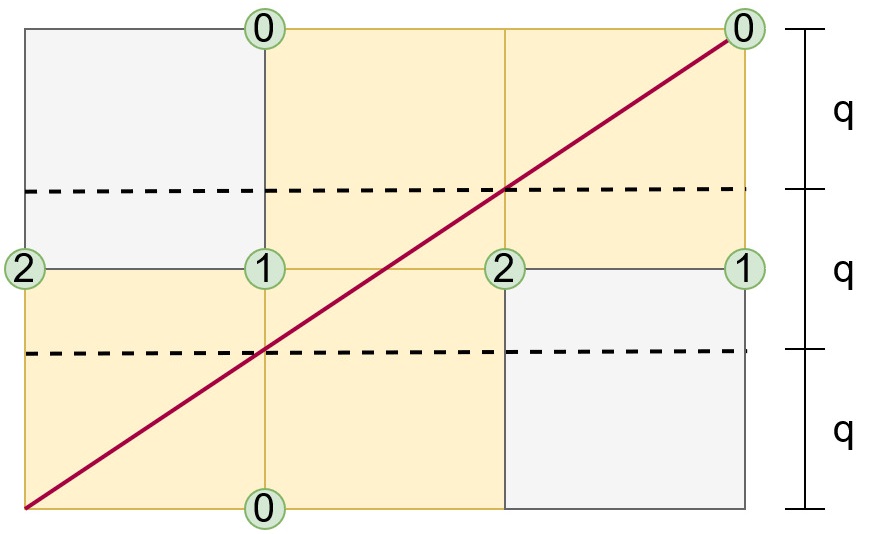
水平移動次數cnt從1開始，不斷遞增直到總移動距離能夠被邊長p整除為止。

若cnt為奇數，則有兩種可能性：

• 若垂直移動次數同為奇數，則碰到接收器1
• 若為偶數，則為接收器0

cnt為偶數只有接收器2一種可能性。
那麼有沒有可能回到出發點？以上圖為例，若要想回到起點，則必須先經過接收器1，所以不必考慮此情況。

class Solution:
    def mirrorReflection(self, p: int, q: int) -> int:
        cnt=1
        
        while (cnt*q)%p!=0:
            cnt+=1
            
        if cnt%2==1 and (cnt*q//p)%2==1:return 1
        if cnt%2==1 and (cnt*q//p)%2==0:return 0
        return 2