LeetCode 435. Non-overlapping Intervals

每日題。正難則反的好例子。

題目

輸入一個區間陣列intervals，其中intervals[i] = [start_i, end_i]。
求最少要刪除幾個區間，才能使所有區間不重疊。

解法

乍看很難知道刪除哪個區間是最佳解。
將問題轉換成：最多可以同時存在幾個不重疊的區間，總數N個扣掉最多重疊數，就可使所有區間不重疊。

將區間以右端點排序，依序遍歷，能保證右方區間的右端點一定大於等於當前區間。
若查當前區間[s,e]的左端點大於等於前一個不重疊區間的右端點last，則代表當前也不重疊，計數+1，更新last。

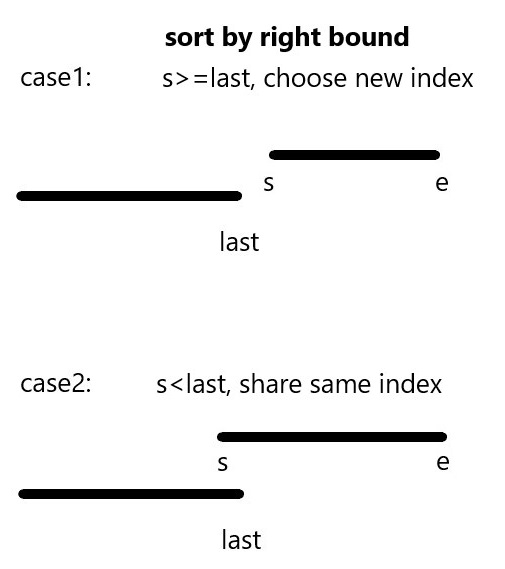
瓶頸在於排序，時間複雜度O(N log N)。
空間複雜度O(1)。

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        N=len(intervals)
        intervals.sort(key=itemgetter(1))
        
        cnt=0
        last=-inf
        for s,e in intervals:
            if s>=last: # case 1
                cnt+=1
                last=e
                
        return N-cnt

當然也可以不轉換問題，就按照原本的題意來做。

同樣以右端點排序，如果當前區間[s,e]要和左方的區間重疊，那必定是s要小於先前的右端點last，需要刪除，所以不更新右端點last；否則以e更新last。

瓶頸在於排序，時間複雜度O(N log N)。
空間複雜度O(1)。

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        N=len(intervals)
        intervals.sort(key=itemgetter(1))
        
        cnt=0
        last=-inf
        for s,e in intervals: # assured e>=last
            if s<last: # overlapped, remove
                cnt+=1
            else: # keep and update right bound
                last=e
                
        return cnt

也可以依左端點排序，同樣計算要刪除的重疊區間數。

較靠右的區間，其左端點一定大於等於先前出現過的其他區間。
因此若[s,e]與先前區間無交集，則e肯定會是最靠右的端點，因此以e更新last；若有交集，則保留右端點較小的，比較不容易和剩下的區間產生重疊。

瓶頸在於排序，時間複雜度O(N log N)。
空間複雜度O(1)。

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        N=len(intervals)
        intervals.sort(key=itemgetter(0))
        
        cnt=0
        last=-inf
        for s,e in intervals: 
            if s>=last: # assured e>=last
                last=e
            else: # overlapped, keep lefter one
                cnt+=1
                last=min(last,e)
            
        return cnt