LeetCode 3553. Minimum Weighted Subgraph With the Required Paths II

May 18, 2025

weekly contest 450。
本次算是圖論專場，Q234 全都是圖論。

題目

https://leetcode.com/problems/minimum-weighted-subgraph-with-the-required-paths-ii/description/

解法

輸入一棵樹，查詢包含任意三點的權重最小子樹。

雖然三個點我不知道怎麼搞，但如果是兩個點就很簡單。
求 a,b 兩點的 lca，分別計算 a,b 與 lca 的距離即可。

相似題：2846. minimum edge weight equilibrium queries in a tree。

回歸正題，三個點怎麼求？
最初本想拿深度較大的兩個點求 lca，再拿 lca 和第三個點求一次。
結果碰到下例就炸了：

edges = [[0,1,10],[2,0,2],[3,2,8]]
querie = [1,3,2]

示意圖

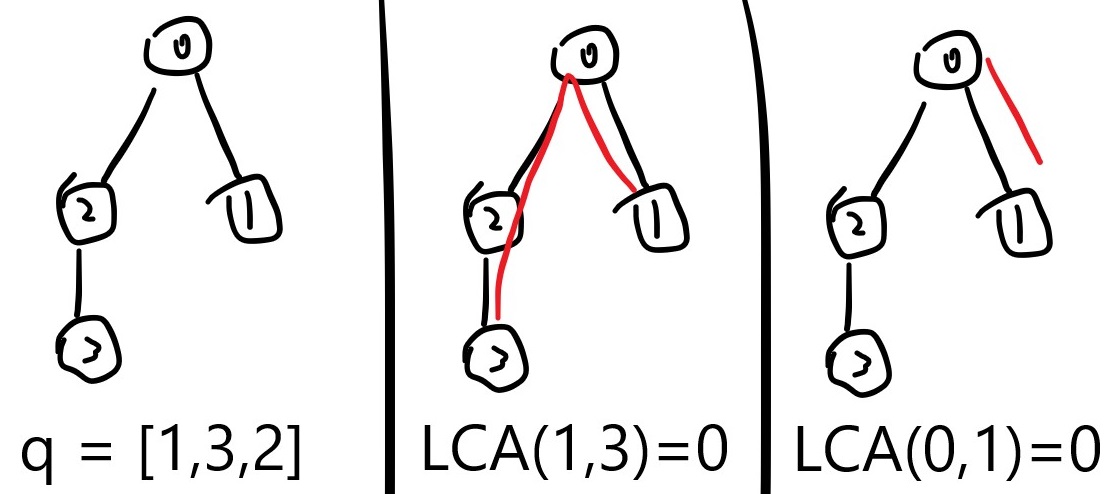
節點 1,2 深度相同，沒有辦法判斷優先順序。
先求 t = lca(1,3) 再求 lca(t, 2) 明顯錯誤，重複走了 [0,1] 這條邊。

不過好險也只有三個點，暴力枚舉 3! = 6 種順序，求最小值就勉強能過了。
有點卡常，如果改用前綴和求距離就會超時，挺玄學的。

時間複雜度 O((N+Q) log N)。
空間複雜度 O(N log N)。

class Solution:
    def minimumWeight(self, edges: List[List[int]], queries: List[List[int]]) -> List[int]:
        N = len(edges) + 1  # 有多少點
        MX = N.bit_length()  # 最大跳躍次數取 log

        # 建圖建樹
        g = [[] for _ in range(N)]
        for a, b, w in edges:
            g[a].append([b, w])
            g[b].append([a, w])

        first_jump_val = [-1] * N
        parent = [-1] * N
        depth = [0] * N

        def dfs(i, fa, dep):
            parent[i] = fa
            depth[i] = dep
            for j, w in g[i]:
                if j == fa:
                    continue
                first_jump_val[j] = w
                dfs(j, i, dep+1)

        dfs(0, -1, 0)

        # f[i][jump]: 從 i 跳 2^jump 次的位置
        # -1 代表沒有下一個點
        f = [[-1]*MX for _ in range(N)]
        val = [[0]*MX for _ in range(N)]

        # 初始化每個位置跳一次
        # 實作細節自行修改
        for i in range(N):
            f[i][0] = parent[i]
            val[i][0] = first_jump_val[i]

        # 倍增遞推
        for jump in range(1, MX):
            for i in range(N):
                temp = f[i][jump-1]
                f[i][jump] = f[temp][jump-1]
                val[i][jump] = val[i][jump-1] + val[temp][jump-1]

        def get_LCA(x, y):
            if depth[x] > depth[y]:
                x, y = y, x

            # 把 y 調整到和 x 相同深度
            cost = 0
            diff = depth[y]-depth[x]
            for jump in range(MX):
                if diff & (1 << jump):
                    cost += val[y][jump]
                    y = f[y][jump]

            # 已經相同
            if x == y:
                return x, cost

            # 否則找最低的非 LCA
            for jump in reversed(range(MX)):
                if f[x][jump] != f[y][jump]:
                    cost += val[x][jump]
                    cost += val[y][jump]
                    x = f[x][jump]
                    y = f[y][jump]

            # 再跳一次到 LCA
            cost += val[x][0] + val[y][0]
            return f[x][0], cost

        def solve(nodes):
            mn = inf
            # 暴力枚舉 6! 種合併順序
            for a, b, c in permutations(nodes, 3):
                lca, cost1 = get_LCA(a, b)
                _, cost2 = get_LCA(lca, c)
                mn = min(mn, cost1 + cost2)
            return mn

        return [solve(q) for q in queries]

發現很多人都不是暴力枚舉，而是使用公式算路徑：

(dist(a,b) + dist(b,c) + dist(c,a)) / 2

來研究這是怎麼推出的。
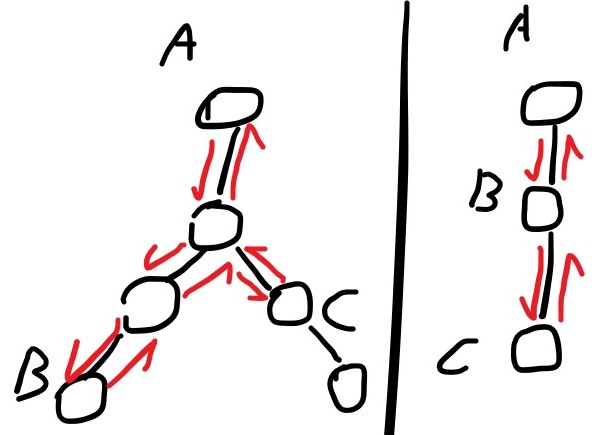
在三個點任意分布時，如果依照 a, b, c, a 的順序走訪，會發現經過的每條邊都被走過兩次。
總距離除 2 即最該子樹的路徑和。

示意圖

順便改用新的 LCA 模板，看起來比舊版順眼。

class Solution:
    def minimumWeight(self, edges: List[List[int]], queries: List[List[int]]) -> List[int]:
        tlca = TreeLCA(edges)

        def solve(a, b, c):
            res = tlca.get_distance(a, b)
            res += tlca.get_distance(b, c)
            res += tlca.get_distance(c, a)
            return res // 2

        return [solve(*q) for q in queries]

class TreeLCA:
    def __init__(self, edges):
        N = len(edges) + 1  # 有多少點
        self.MX = N.bit_length()  # 最大跳躍次數取 log
        # 建圖
        g = [[] for _ in range(N)]
        for a, b, w in edges:
            g[a].append([b, w])
            g[b].append([a, w])
        # 建樹 樹上前綴和
        self.parent = [-1] * N
        self.depth = [0] * N
        self.ps = [0] * N

        def dfs(i, fa, dep):
            self.parent[i] = fa
            self.depth[i] = dep
            for j, w in g[i]:
                if j == fa:
                    continue
                self.ps[j] = self.ps[i] + w
                dfs(j, i, dep+1)
        dfs(0, -1, 0)
        # f[i][jump]: 從 i 跳 2^jump 次的位置
        # -1 代表沒有下一個點
        self.f = [[-1] * self.MX for _ in range(N)]
        # 初始化每個位置跳一次
        for i in range(N):
            self.f[i][0] = self.parent[i]
        # 倍增遞推
        for jump in range(1, self.MX):
            for i in range(N):
                temp = self.f[i][jump-1]
                if temp != -1:  # 必須存在中繼點
                    self.f[i][jump] = self.f[temp][jump-1]

    def get_LCA(self, x, y):
        depth = self.depth
        f = self.f
        if depth[x] > depth[y]:
            x, y = y, x
        # 把 y 調整到和 x 相同深度
        diff = depth[y] - depth[x]
        for jump in range(self.MX):
            if diff & (1 << jump):
                y = f[y][jump]
        # 已經相同
        if x == y:
            return x
        # 否則找最低的非 LCA
        for jump in reversed(range(self.MX)):
            if f[x][jump] != f[y][jump]:
                x = f[x][jump]
                y = f[y][jump]
        # 再跳一次到 LCA
        return f[x][0]

    def get_distance(self, x, y):
        lca = self.get_LCA(x, y)
        return self.ps[x] + self.ps[y] - self.ps[lca]*2

路徑 a,b,c,a 起終點相同，稱做迴路 (circuit)。
一般來說迴路沒有起終點之外的限制。

有種特殊的迴路，叫做歐拉迴路 (Eulerian circuit)。
不僅要求起終點相同，且每個邊只能走一次。
但不限制頂點經過幾次。

在連通的無向圖中，歐拉迴路的必要條件是有兩種：

正好兩個頂點的度數是奇數
所有頂點的度數是偶數

在剛才樹上的迴路，每條邊都走了兩次。
把樹上每條邊都變成兩條，就滿足了第二種條建。其實正是歐拉迴路。

歐拉迴路可以保證走的路徑不重複 (原本的邊都變成兩條)，才能保證答案為迴路路徑和除 2 的正確性。

原題中 3 個節點的子樹，其實不管怎樣排都是一條鍊，任選出發點都可以滿足歐拉迴路。
但改查詢 4 個以上 節點最小子樹，那原本的遍歷順序就會出錯。

例如：

edges = [[A,B],[A,D],[B,C],[D,E]]
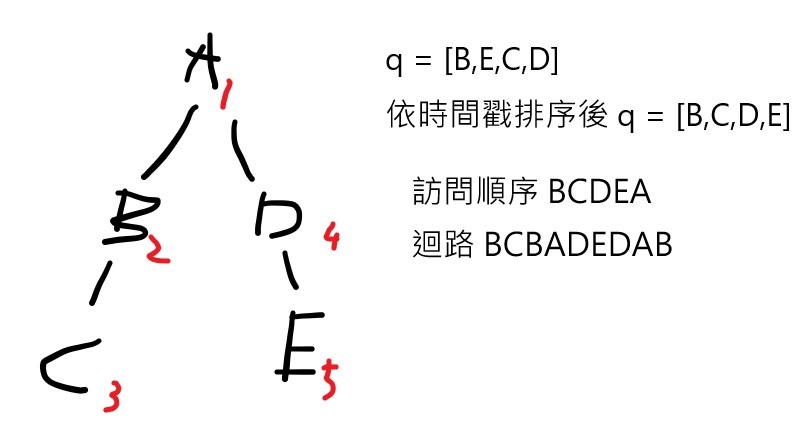
query = [B,E,C,D]

若按照原本 B,E,C,D,B 的順序走，會發現某些部分多走了。

實際路線 BADEDABCBADAB
不是歐拉迴路

B,C 在左子樹中，而 D,E 在右子樹。
更好的順序應該是 query 改成 [C,B,D,E]，然後按照 C,B,D,E,C 走迴路：

實際路線 CBADEDABC
是歐拉迴路

問題轉換成：

在查詢的若干個節點中求歐拉迴路路徑和

從剛才的正確順序中不難看出，應該按照相同子樹順序來訪問目標節點。
說到子樹很多同學應該會想到 dfs 時間戳。
非常巧的，其實 dfs 遍歷的順序正好每條邊各出入一次，類似於歐拉迴路。

只要把目標節點按照 dfs 時間戳排序後，依序訪問迴路即可。

示意圖

mocowcow

題目

解法