LeetCode 3548. Equal Sum Grid Partition II
weekly contest 449。
edge case 放在 hidden case,太壞了。
題目
https://leetcode.com/problems/equal-sum-grid-partition-ii/description/
解法
大致上和 Q2 差不多。
只是改成可以刪除至多一個格子,並且刪除後的所有格子要互相連通。
題目只說到劃分後是非空子矩陣,但沒提到刪除後是否可以為空。
我在這邊想了好久,其實結論很簡單。
格子中的值都是正整數,不管是否允許刪除後為空,都不可能使得空子矩陣和另一半的和相同。
根本不用管。
和 Q2 一樣可以利用對稱性,只討論水平切的情況:
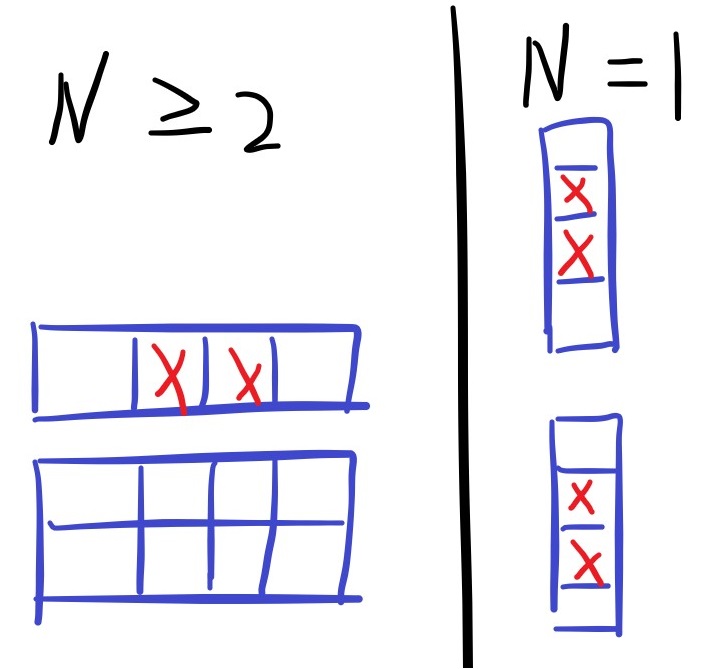
在矩陣長寬至少為 2 的一般情況下,只有兩種情況會在刪除後不連通:
- 上半段只有一列,且刪了非頭尾的元素
- 下半段只有一列,且刪了非頭尾的元素
換句話說,只要下列滿足任一條件則不影響連通:
- 子陣列高至少 2
- 子陣列高為 1,但是刪最左邊或最右邊
分類討論三種答案情況:
- up == down,不用刪
- up > down,若 (up-down) 存在於上半段,且不破壞連通性
- up < down,若 (down-up) 存在於下半段,且不破壞連通性
我們只需要在遍歷過程中維護上下半段剩餘的元素即可。
別忘記處理特殊案例 N = 1 。
當原矩陣呈一條直線時,分割後的兩個子矩陣也是直線。
所以兩個子矩陣只能刪除最上面或是最下面的部分,否則會破壞連通性。
時間複雜度 O(MN)。
空間複雜度 O(MN)。
class Solution:
def canPartitionGrid(self, grid: List[List[int]]) -> bool:
trans = [list(row) for row in zip(*grid)]
return solve(grid) or solve(trans)
def solve(a):
M, N = len(a), len(a[0])
d2 = Counter()
down = 0
for row in a:
for x in row:
d2[x] += 1
down += x
up = 0
d = Counter()
for i in range(M-1):
for j in range(N):
x = a[i][j]
up += x
d[x] += 1
down -= x
d2[x] -= 1
# 不刪
if up == down:
return True
# 刪上面
if up > down:
delta = up - down
if d[delta] > 0:
# 特判 M x 1
if N == 1:
if a[0][0] == delta or a[i][0] == delta:
return True
continue
if i > 0 or a[0][0] == delta or a[0][-1] == delta:
return True
# 刪下面
if up < down:
delta = down - up
if d2[delta] > 0:
# 特判 M x 1
if N == 1:
if a[-1][0] == delta or a[i+1][0] == delta:
return True
if i < M-2 or a[-1][0] == delta or a[-1][-1] == delta:
return True
return False
其實不只水平垂直可以複用同一個邏輯,連水平切裡面上下半段也可以複用。
只需要實作檢查上半段的邏輯,將矩陣上下翻轉,就可以刪上下段了。
class Solution:
def canPartitionGrid(self, grid: List[List[int]]) -> bool:
# 1. 水平切
# 2. 右轉 90 度後水平切 = 垂直切
trans = [list(row) for row in zip(*grid)]
return solve(grid) or solve(trans)
def solve(a):
# 1. 刪上半段
# 2. 上下翻轉後刪上半段 = 刪下半段
return delete_up(a) or delete_up(a[::-1])
def delete_up(a):
M, N = len(a), len(a[0])
down = 0
for row in a:
for x in row:
down += x
up = 0
d = Counter()
for i in range(M-1):
for j in range(N):
x = a[i][j]
up += x
d[x] += 1
down -= x
# 不刪
if up == down:
return True
# 刪上面
if up > down:
delta = up - down
if d[delta] > 0:
# 特判 M x 1
if N == 1:
if a[0][0] == delta or a[i][0] == delta:
return True
continue
if i > 0 or a[0][0] == delta or a[0][-1] == delta:
return True
return False