LeetCode 3500. Minimum Cost to Divide Array Into Subarrays

biweekly contest 153。
應該算是初見殺，第一次碰到這種很難想出解法。

題目

https://leetcode.com/problems/minimum-cost-to-divide-array-into-subarrays/description/

解法

又是劃分子陣列、又是最小成本，很容易想到劃分型 dp。

記 ps 為 nums 的前綴和，ps_cost 為 cost 的前綴和。
每劃分出 nums[l..r] 的成本為：

(ps[r] + k*i) * (ps_cost[r] - ps_cost[l-1])

隨著劃分次數增加，i 也會跟著增加。
定義 dp(l, i)：將 nums[l..] 劃分成若干子陣列的最小成本。
枚舉劃分的右端點 r，以 nums[l..r] 成本 + dp(r, i+1) 更新最小值。

但是光狀態數就有 O(N^2) 個，每個狀態需轉移 O(N) 次。
對於本題 N = 1000 來說很明顯超時。
狀態裡面多了一個 i 非常麻煩。

---

試著把成本公式展開：

(ps[r] + k*i) * (ps_cost[r] - ps_cost[l-1])
ps[r]*(ps_cost[r] - ps_cost[l-1]) + k*i*(ps_cost[r] - ps_cost[l-1])

左半邊跟 i 解耦，但右半邊還是跟 i 綁定，乍看之下沒有解決問題，但是代入例子就會得到很奇妙的性質。

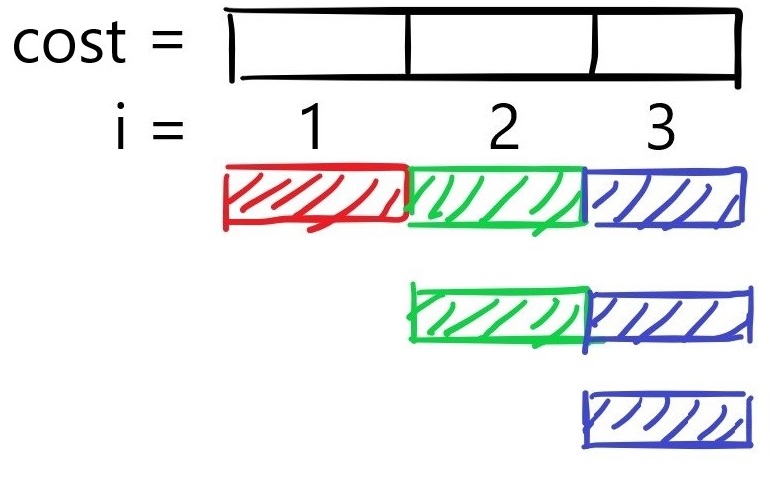
試將 nums 分成三段 [l1..r1], [l2..r2], [l3..r3]：

第一段成本 k*1*ps(cost[l1..r1])
第二段成本 k*2*ps(cost[l2..r2])
第一段成本 k*3*ps(cost[l3..r3])

拼湊起來正好得到：

k* ps(cost[l1..r3])
k* ps(cost[l2..r3])
k* ps(cost[l3..r3])

也就是說，不管當前劃分第幾段子陣列，可以改成計算 cost 的後綴和。
這時候 i 是多少已經無所謂了。

時間複雜度 O(N^2)。
空間複雜度 O(N)。

class Solution:
    def minimumCost(self, nums: List[int], cost: List[int], k: int) -> int:
        N = len(nums)
        ps = list(accumulate(nums, initial=0))
        ps_cost = list(accumulate(cost, initial=0))

        @cache
        def dp(i):
            if i == N:
                return 0
            res = inf
            for j in range(i, N):
                sub_cost = ps[j+1] * (ps_cost[j+1] - ps_cost[i])
                sub_cost += k * (ps_cost[N] - ps_cost[i])  # suffix sum of cost
                res = min(res, dp(j+1) + sub_cost)
            return res

        return dp(0)