LeetCode 3494. Find the Minimum Amount of Time to Brew Potions

March 23, 2025

weekly contes 442。
這題是真的鳥，本身就不太好寫，還給個垃圾測資。

期望 O(N^2) 的解法卻給 N = 5000，我都不知道他想不想讓人通過。
python 開個 N * N 陣列值接爆 MLE，還得空間壓縮才能過。

題目

https://leetcode.com/problems/find-the-minimum-amount-of-time-to-brew-potions/description/

解法

題目有點繞，反正就是依序製造藥水 mana[j]。每個藥水都要依序傳遞給 skill[i] 的人加工，耗時 mana[j] * skill[i]。
求最早的完成時間。

藥水需要依序動工，但可以有若干個同時處於加工狀態。
但每個人手上只能有一瓶水。

且藥水一但動工，必須無縫接軌交到每個人手上，不能放著等待。
例如：skill[i] 在 10 完成加工，但是 skill[i+1] 還在忙，要到 12 秒才有空。
這樣藥水就等待兩秒，不合法。

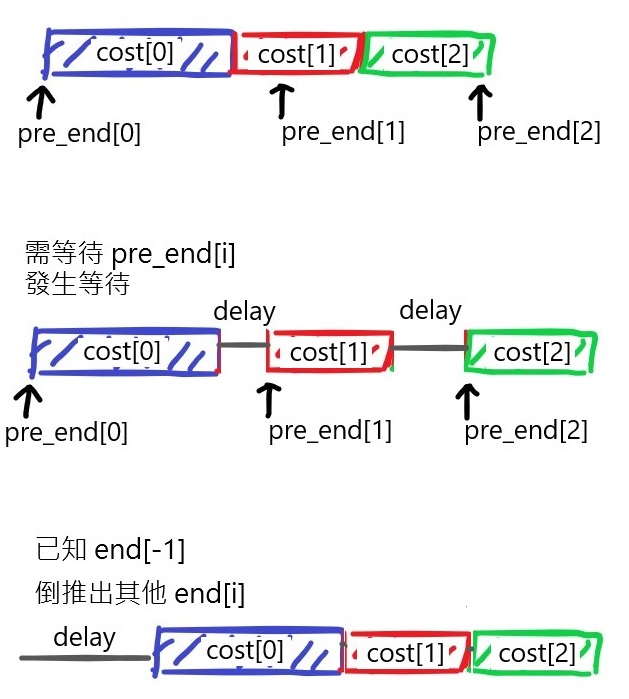
設 pre_end[i] 為第 i 個人上次的完工時間，同時為本次的可開工時間。
再設 want_start[i] 為本次第 i 個人的期望開工時間。

want_start[i] 越早越好，第一個人的開工時間為 pre_end[0]。
先忽略等待，遞推其他人的開工時間。下一個人的開工時間為上一個人的結束時間：

want_start[i] = want_start[i] + cost[i]

這時我們有期望時間和實際時間，兩個的差就是等待時間。
求出每個人的等待時間：

delay[i] = pre_end[i] - want_start[i]

max(delay[i])，即為本次的最大等待時間。
第一個人開工前先等待，然後就可以依序加工，更新結束時間。

時間複雜度 O(MN)。
空間複雜度 O(N)。

class Solution:
    def minTime(self, skill: List[int], mana: List[int]) -> int:
        N = len(skill)

        # 上次結束時間
        pre_end = [0] * N
        for x in mana:
            # 預處理製作時間
            cost = [x*y for y in skill]

            # 假設沒有衝突，第一個人的 "期望開始時間" 等於 "上次結束時間"
            want_start = [0] * N
            want_start[0] = pre_end[0]
            # 之後依序加工，算出下一個人的 "期望開始時間"
            for i in range(1, N):
                want_start[i] = want_start[i-1] + cost[i-1]

            # "期望開始時間" 與 "上次結束(實際開始時間)" 之差，即閒置時間
            # 求本次最大等待時間 delay
            delay = max(e-s for e, s in zip(pre_end, want_start))

            # 為了避免藥水閒置，第一個人要先等待 delay 秒，才開始製作
            pre_end[0] = want_start[0] + delay + cost[0]
            # 之後依序加工，算出下一個人的 "實際結束時間"
            for i in range(1, N):
                pre_end[i] = pre_end[i-1] + cost[i]

        return pre_end[-1]       

提供另外一種思路。

假設允許閒置等待，只有最後一個人的完工時間會是正確的，但前方可能會有若干個閒置段。
既然我們知道每個人的工時，那麼可以從最後一個人的完工時間倒著扣掉工時。

示意圖

class Solution:
    def minTime(self, skill: List[int], mana: List[int]) -> int:
        N = len(skill)

        # 上次結束時間
        pre_end = [0] * N
        for x in mana:
            # 預處理製作時間
            cost = [x*y for y in skill]

            # 假設允許等待
            # 先算出包含等待的完工時間
            last_end = pre_end[0] + cost[0]
            for i in range(1, N):
                last_end = max(last_end, pre_end[i]) + cost[i]

            # 至少最後一人是正確的最早完工時間
            # 倒著往回推算出其他人的完工時間
            # 而等待時間會自動移到開工之前
            pre_end[-1] = last_end
            for i in reversed(range(N-1)):
                last_end[i] = last_end[i+1] - cost[i+1]

        return pre_end[-1]

mocowcow

題目

解法