LeetCode 3486. Longest Special Path II

March 18, 2025

biweekly contest 152。
從頭開始寫的話很難，但是拿原題修改下倒還可以接受，只是取變數還是很繞口。

題目

https://leetcode.com/problems/longest-special-path-ii/description/

解法

原題 3425. longest special path。
兩題幾乎一樣，原本是路徑上的顏色都只出現一次，改成至多一個顏色出現兩次。

注意：是至多一個顏色出現兩次。
注意：是至多一個顏色出現兩次。
注意：是至多一個顏色出現兩次。

很重要所以說三次，別誤會成每個顏色至多出現兩次。

老樣子，從特殊到一般，先從一條直線的樹開始思考。

原題只維護每個顏色上次出現的位置 last，並以 last + 1 更新路徑起點。
但本題可以容忍一次，只有在第二種顏色出現兩次次才要更新起點。
所以需要多一個變數 pre_last 紀錄上次出現兩次的顏色的上次出現位置。
為了方便識別，本次出現兩次的顏色的上次出現位置改叫 cur_last。

舉例：

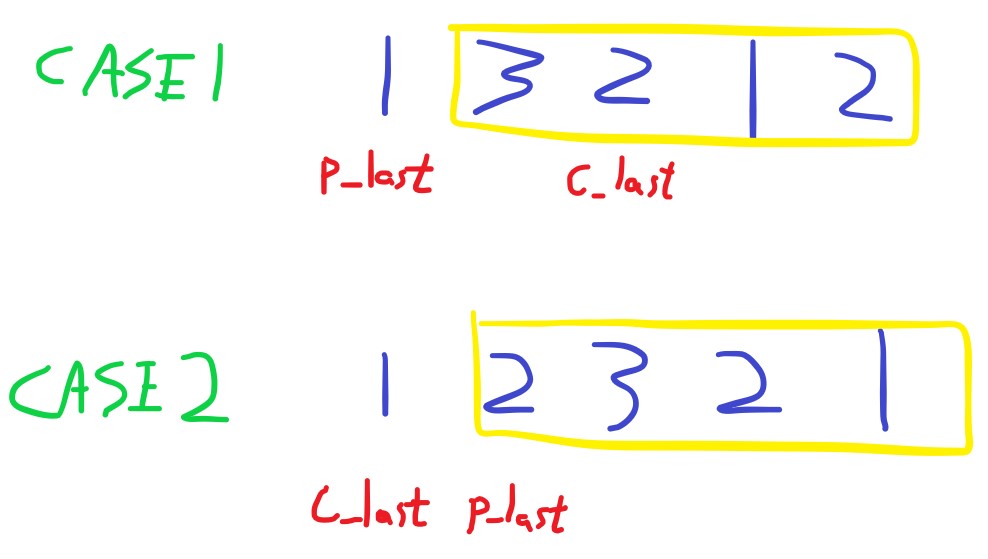
path = [1,3,2,1]
1 出現兩次。1 上次出現的位置是 path[0]，記 pre_last = 0
加上 [2] 變成 [1,3,2,1,2]
2 也出現兩次。2 上次出現位置是 path[2]，記 cur_last = 2

這時不滿足限制，要讓路徑中減少一個 1 或是 2。兩種選擇：

如果要減少 1，則要刪除 [1]，剩下 [3,2,1,3]
如果要減少 2，則要刪除 [1,3,2]，剩下 [1,2]

前者剩餘路徑更長，更能夠得到較大的路徑和。
因此貪心地選擇較小的 last，記做 mn_last = min(pre_last, cur-last)。
並以 mn_last + 1 更新路徑起點。

剛才我們刪除了 path[..mn_last] 這段，確保剩下的 path[mn_last+1..] 至多只有一個顏色重複。
但剩下的重複顏色並非 mn_last+1，而是 mx_last。
mx_last 即為下一次遞迴的 pre_last。

示意圖

最後討論遞迴入口。
最初沒有顏色時，自然沒有 pre_last。
而初始的路徑起點是 0。我們會以 pre_last + 1 更新起點，故設為 -1，避免改變路徑起點。

時間複雜度 O(N)。
空間複雜度 O(N)。

class Solution:
    def longestSpecialPath(self, edges: List[List[int]], nums: List[int]) -> List[int]:
        N = len(edges) + 1
        g = [[] for _ in range(N)]
        for a, b, l in edges:
            g[a].append([b, l])
            g[b].append([a, l])

        ans_len = 0
        ans_node = 1
        path_len = [0] * N  # 到各深度時的路徑長度和
        last = defaultdict(list)  # 各節點顏色的上一次出現深度

        # "前次顏色" 的上次出現位置 pre_last
        # 最初不存在，初始值 -1
        def dfs(i, fa, depth, start_depth, pre_last):
            nonlocal ans_len, ans_node
            color = nums[i]

            ## 與 3425 不同處
            # "當前顏色" 的上次出現位置 curr_last
            # 若不存在則為 -1
            curr_last = last[color][-1] if last[color] else -1
            mn_last = min(pre_last, curr_last)
            mx_last = max(pre_last, curr_last)
            start_depth = max(start_depth, mn_last + 1)  # 以較小的 last 更新起點

            # 更新答案
            valid_len = path_len[depth] - path_len[start_depth]
            valid_node = depth - start_depth + 1
            if valid_len > ans_len:
                ans_len = valid_len
                ans_node = valid_node
            elif valid_len == ans_len and valid_node < ans_node:
                ans_node = valid_node

            last[color].append(depth)  # 紀錄當前顏色出現的深度，供子節點判斷
            for j, l in g[i]:
                if j == fa:
                    continue
                path_len[depth+1] = path_len[depth] + l
                dfs(j, i, depth+1, start_depth, mx_last)  # 較大的 last 做為新的 pre_last
            last[color].pop()  # 遞迴結束，恢復現場

        dfs(0, -1, 0, 0, -1)

        return [ans_len, ans_node]

mocowcow

題目

解法