LeetCode 3382. Maximum Area Rectangle With Point Constraints II

December 9, 2024

weekly contest 427。

題目

有 n 個座標點在無限平面上。
輸入整數陣列 xCoord 和 yCoord，其中 (xCoord[i], yCoord[i]) 代表第 i 個點的座標。

你的目標是找到最大的矩形面積，滿足：

四個頂點必須是陣列中的座標點。
在矩形內部或是邊界上不可有其他點。
矩形的邊與座標軸平行。

回傳最大面積，若不存在則回傳 -1。

解法

跟 Q2 差不多，只是點的數量變成 2e5，座標值域達 8e7，有夠大。

看個幾個大神的作法，挑一種最好理解的方式。

首先將點以 x 軸遞增排序，能保證相同 x 軸的點都會聚集在一起。
然後再以 y 軸遞增排序，能 x 軸的相同的點，會以 y 軸遞增的順序相鄰。
排序後，枚舉所有點作為矩形的右上角 (x2, y2)，保證先前遇過的所有點都在左方或是正下方。

示意圖

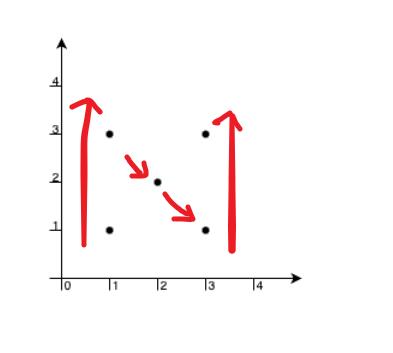
若當前 points[i] 點 (x2, y2) 的正下方存在其他點，必為 (x2, y1)，排序後的索引是 points[i-1]。
此時確定矩形的上下界為 y2, y1。

雖然無法直接算出矩形內的點，也不知道左邊界在哪裡。
但是以左下角 (0, y1) 到右上角 (x2, y2)，只需要一維的區間查詢資料結構即可。

示意圖

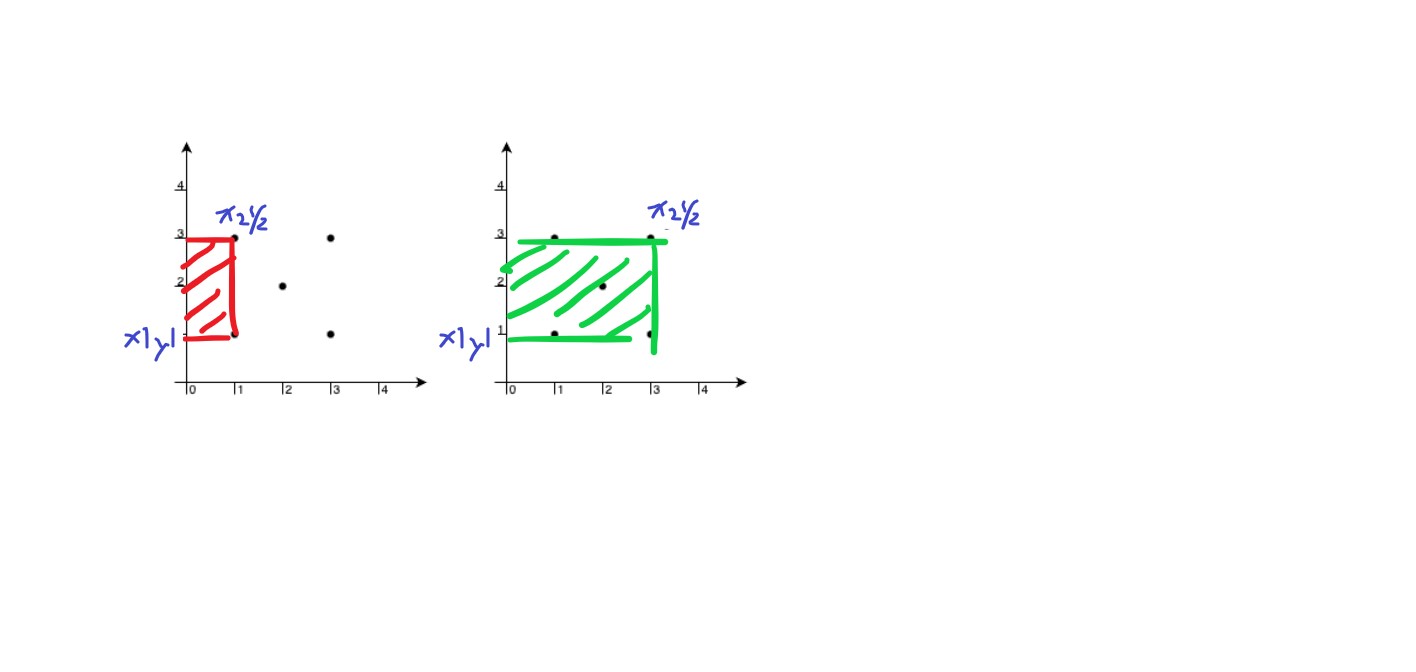
按照這個順序，只要找到前一個上下界相同的矩形，比對一下點的數量，就知道矩形內有多少點。
例如：

前一個矩形的右上、右下為 (x1, y2), (x1, y1)，有 4 個點。
當前矩形的右上、右下為 (x2, y2), (x2, y1)，有 6 個點。

根據矩形的枚舉方式，右上、右下點之間必不含其他點。若正好多出 2 點可保證矩形內沒有其他點，以此面積更新答案。

在枚舉右上角的過程中，還需要逐步將點加入資料結構。
每次只會影響一個 y 軸，只需要單點修改，可以選擇用樹狀陣列。
而且 y 軸的值域過大，需要做離散化。

找到右下角時，先檢查是否有前一個矩形、點數變化判斷，嘗試更新答案。

最後將當前矩形的點數與 x 座標保存，以供後續使用。

時間複雜度 O(N log N)。
空間複雜度 O(N)。

class Solution:
    def maxRectangleArea(self, xCoord: List[int], yCoord: List[int]) -> int:
        N = len(xCoord)
        sorted_y = sorted(set(yCoord))
        mp_y = {x: i for i, x in enumerate(sorted_y)}
        points = list(zip(xCoord, yCoord))
        points.sort()  # sort by x-axis, then by y-axis

        bit = BIT(N+5)
        ans = -1
        # previous rect area with (y1, y2)
        # which rightbound is x1, and has p_cnt points
        # seen[(y1, y2)] = [x1, p_cnt]
        seen = {}
        for i, (x2, y2) in enumerate(points):
            # count point (x2, y2)
            y2 = mp_y[y2]
            bit.update(y2, 1)

            # find rectangle
            # must find lower right (x2, y1) first
            if i > 0 and points[i-1][0] == x2:
                y1 = mp_y[points[i-1][1]]
                p_cnt = bit.query_range(y1, y2)
                key = (y1, y2)

                # check if rect valid
                if key in seen and seen[key][1] + 2 == p_cnt:
                    x1 = seen[key][0]
                    w = x2 - x1
                    h = sorted_y[y2] - sorted_y[y1]
                    ans = max(ans, w*h)

                # update points count
                seen[key] = (x2, p_cnt)

        return ans


class BIT:
    """
    tree[0]代表空區間，不可存值，基本情況下只有[1, n-1]可以存值。
    offset為索引偏移量，若設置為1時正好可以對應普通陣列的索引操作。
    """

    def __init__(self, n, offset=1):
        self.offset = offset
        self.tree = [0]*(n+offset)

    def update(self, pos, val):
        """
        將tree[pos]增加val
        """
        i = pos+self.offset
        while i < len(self.tree):
            self.tree[i] += val
            i += i & (-i)

    def query(self, pos):
        """
        查詢[1, pos]的前綴和  
        """
        i = pos+self.offset
        res = 0
        while i > 0:
            res += self.tree[i]
            i -= i & (-i)
        return res

    def query_range(self, i, j):
        """
        查詢[i, j]的前綴和
        """
        return self.query(j)-self.query(i-1)

mocowcow

題目

解法