LeetCode 3311. Construct 2D Grid Matching Graph Layout

October 7, 2024

weekly contest 418。

題目

輸入二維整數陣列 edges，代表 n 節點的無向圖，其中 edges[i] = [u_i, v_i]，代表 u_i 和 v_i 之間存在一條邊。

構造一個滿足以下條件的二維矩陣：

矩陣中每個格子正好對應 0 倒 n - 1 的所有節點
若且唯若兩個節點在 edges 中有連邊，則對應的兩個格子在舉陣中相鄰 (橫豎皆可)

題目保證至少有一個矩陣可以滿足條件。
回傳任意一種滿足條件的矩陣。

解法

節點的連邊數量稱做度數。
對於二維矩陣來說，節點的度數可能是 0~4。
但本題只少會有兩個節點，因此實際上可能出現的度數只有 1~4。

示意圖

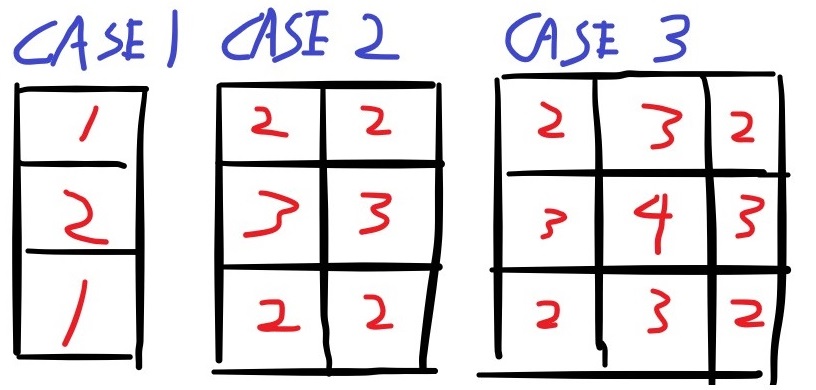
大部分同學應該看圖例就很像拼圖。

但本題只說有幾塊，並沒有提供完整拼圖的尺寸。
我們需要根據拼圖的種類來自行判斷，如上圖。
分類討論三種形況：

若存在度數 1 的節點，代表只有 1 行 (列)。
否則，若不存在度數 4 的節點，代表只有 2 行 (列)。
否則都是一般情形，行列數至少有 3。

拼拼圖最簡單的方式是從角落開始，然後拚完第一列，再沿著拚好的邊緣繼續展延。
只要拚好第一列，剩下的事情就簡單了。

拼圖不管你如何翻轉、旋轉，都還是能拚起來，因此不必在意擺放的角度。
為了我們操作方便起見，一律由上至下、由左至右構造矩陣。
首先找到第一列：

case 1：左上角隨便塞一個度數 1 的節點就行
case 2：左上角隨便塞一個度數 2 的節點。
然後從當前節點的鄰居中，選擇度數同為 2 的節點。
case 3：左上角隨便塞一個度數 2 的節點。
第一列的節點度數應該是 233..332。
不斷從當前節點的鄰居中選擇沒選過且度數不為 4 的節點。

構造完第一列之後，就能確定此矩陣的行數，並推算出正確列數。
從第二列開始，只要遍歷上一列的節點，其鄰節點必定只剩一個沒選過，直接選下去就對了。

時間複雜度 O(N + M)。
空間複雜度 O(N + M)。

class Solution:
    def constructGridLayout(self, n: int, edges: List[List[int]]) -> List[List[int]]:
        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)

        degree_group = [[] for _ in range(5)]
        for i in range(n):
            degree_group[len(g[i])].append(i)
        
        # 1 col
        if degree_group[1]:
            a = degree_group[1][0]
            first_row = [a]

        # 2 cols
        elif not degree_group[4]:
            a = degree_group[2][0]
            for b in g[a]:
                if len(g[b]) == 2:
                    break
            first_row = [a, b]

        # 3+ cols
        else:
            a = degree_group[2][0]
            first_row = [a] # first col
            prev = a
            curr = g[a][0]
            while len(g[curr]) == 3: # middle cols
                first_row.append(curr)
                for adj in g[curr]:
                    if adj != prev and len(g[adj]) < 4: # degree 2 or 3
                        prev = curr
                        curr = adj
                        break
            first_row.append(curr) # last col

        col_sz = len(first_row)
        row_sz = n // col_sz
        ans = [[] for _ in range(row_sz)]
        ans[0] = first_row

        # mark first row as visited
        vis = [False] * n
        for x in first_row:
            vis[x] = True

        # fill 2+ rows
        for r in range(1, row_sz):
            for upper in ans[r-1]: # connect from upper element
                for adj in g[upper]: 
                    if not vis[adj]: # only 1 unvisited
                        vis[adj] = True
                        ans[r].append(adj)
                        break

        return ans

mocowcow

題目

解法