LeetCode 3244. Shortest Distance After Road Addition Queries II

August 5, 2024

weekly contest 409。

題目

輸入整數 n 以及二維整數陣列 queries。

有 n 個城市，編號分別由 0 到 n - 1。
最初，所有編號滿足 0 <= i < n - 1 的城市 i，都存在一條通往城市 i + 1 的無向道路。

queries[i] = [u_i, v_i] 代表新增一條 u_i 往 v_i 的無向道路。
對於每次查詢，你必須在新增道路後，查詢城市 0 到城市 n - 1 的最短距離。

保證沒有任何查詢滿足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。

回傳陣列 answer，其中 answer[i] 代表第 i 次查詢的結果。

解法

和上一題比起來，除了測資範圍變大之外，還多了個限制：

任意兩個路徑之間不可能部分交集，只能是無交集或是包含

因為不存在交錯的路徑，這代表可以貪心的選擇前往編號最大的城市 j。

換句話說，每當新增了一條路徑 (x, y)，則界於 [x+1, y-1] 區間內的所有城市就不會訪問到了。
我們只需要維護哪些城市被刪除，而答案就是剩餘的城市數減去 1。

每次新增路徑後，需要區間修改連續的城市，並且區間查詢所有城市中有哪些被刪除。
此處使用線段樹。

時間複雜度 O(Q log n)。
空間複雜度 O(n)。

class Solution:
    def shortestDistanceAfterQueries(self, n: int, queries: List[List[int]]) -> List[int]:
        seg = SegmentTree(n)
        ans = []
        for x, y in queries:
            if x + 1 <= y - 1:
                seg.update(1, 0, n-1, x+1, y-1, 1)
            ans.append(n - seg.tree[1] - 1)

        return ans


class SegmentTree:

    def __init__(self, n):
        self.tree = [0]*(n*4)
        self.lazy = [0]*(n*4)

    def op(self, a, b):
        """
        任意符合結合律的運算
        """
        return a+b

    def push_down(self, id, L, R, M):
        """
        將區間懶標加到答案中
        下推懶標記給左右子樹
        """
        if self.lazy[id]:
            self.tree[id*2] = (M-L+1)
            self.lazy[id*2] = 1
            self.tree[id*2+1] = (R-M)
            self.lazy[id*2+1] = 1
            self.lazy[id] = 0

    def push_up(self, id):
        """
        以左右節點更新當前節點值
        """
        self.tree[id] = self.op(self.tree[id*2], self.tree[id*2+1])

    def update(self, id, L, R, i, j, val):
        """
        區間更新
        對[i, j]每個索引都變成 1
        """
        if i <= L and R <= j:  # 當前區間目標範圍包含
            self.tree[id] = (R - L + 1)
            self.lazy[id] = 1
            return
        M = (L+R)//2
        self.push_down(id, L, R, M)
        if i <= M:
            self.update(id*2, L, M, i, j, val)
        if M < j:
            self.update(id*2+1, M+1, R, i, j, val)
        self.push_up(id)

其實線段樹有點大材小用，拿有序集合維護未被刪除的點即可。
每次加入新路徑後，二分找到第一個和最後一個要被刪除的位置，從集合中刪除即可。

時間複雜度 O(Q log n)。
空間複雜度 O(n)。

from sortedcontainers import SortedList as SL
class Solution:
    def shortestDistanceAfterQueries(self, n: int, queries: List[List[int]]) -> List[int]:
        sl = SL(range(n))
        ans = []
        for x, y in queries:
            i = sl.bisect_left(x + 1)
            j = sl.bisect_left(y)
            for _ in range(j - i):
                sl.pop(i)
            ans.append(len(sl) - 1)

        return ans

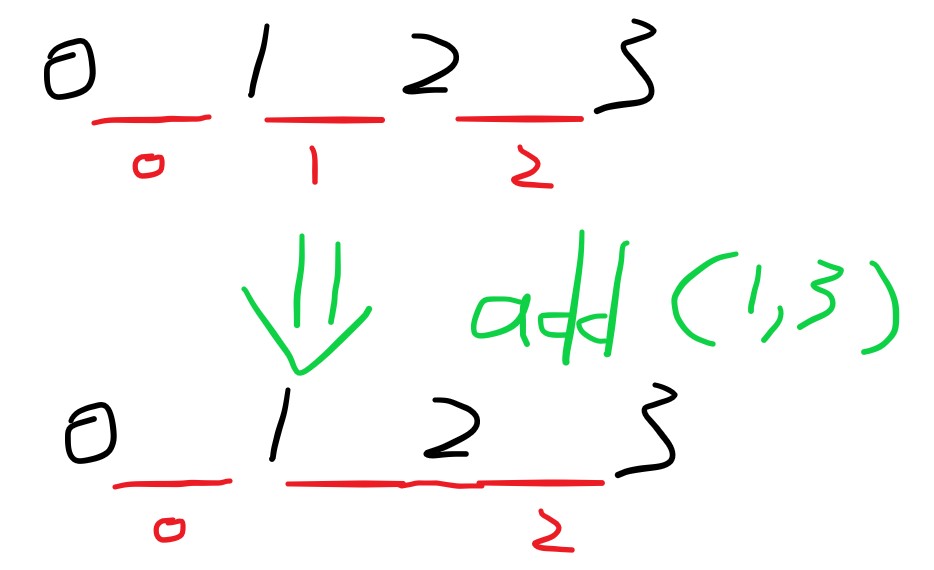
另一個思路是把城市之間的路徑當作是區間節點，每次新增新路徑的時候相當於把區間合併。
這時候可以使用並查集。

最初相當於有 n-1 個區間，每次新增 (x, y) 路徑時，把編號為 [x, y-1] 的節點都指向 y-1。
每次成功合併記得減少區間計數，並在合併結束後將剩餘區間數加入答案。

示意圖

雖然只使用路徑壓縮並查集，每次合併理應是 O(log n)。
但是合併區間的過程當中，都會先調用 find 而把高度攤平，其實只有 O(1)。

時間複雜度 O(Q + n)。
空間複雜度 O(n)。

class Solution:
    def shortestDistanceAfterQueries(self, n: int, queries: List[List[int]]) -> List[int]:
        uf = UnionFind(n - 1)
        part = n - 1
        ans = []
        for x, y in queries:
            l = uf.find(x)
            r = uf.find(y - 1)
            while l != r:
                part -= 1
                uf.union(l, r)
                l = uf.find(l + 1)
            ans.append(part)

        return ans


class UnionFind:
    def __init__(self, n):
        self.parent = [0] * n
        for i in range(n):
            self.parent[i] = i

    def union(self, x, y):
        px = self.find(x)
        py = self.find(y)
        if px != py:
            self.parent[px] = py

    def find(self, x):
        if x != self.parent[x]:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

mocowcow

題目

解法