雜事、解題紀錄

biweekly contest 136。
個人覺得比 Q3 還簡單一些。

題目

輸入一棵 n 節點的無向樹，節點編號分別從 0 到 n - 1。
輸入長度 n - 1 的二維整數陣列 edges，其中 edges[i] = [ui, vi]，代表 ui 和 vi 之間存在一條無向邊。

最初，所有節點都是未標記的。對於每個節點 i：

  • 若 i 是奇數，在時間 x - 1 時出現第一個被標記的相鄰節點後，則 i 會在時間 x 被標記。
  • 若 i 是偶數，在時間 x - 2 時出現第一個被標記的相鄰節點後，則 i 會在時間 x 被標記。

回傳陣列 time，其中 times[i] 代表以在時間 t = 0 時標記節點 i，使得所有節點都被標記的所需時間。

注意：每個 times[i] 都是獨立的。

解法

標記流程描述有點怪，換個更容易理解的說法。
若節點 i 在時間 x 被標記，則對於相鄰且未標記的節點 j：

  • 若 j 是奇數，則在 1 秒後被標記。
  • 若 j 是偶數，則在 2 秒後被標記。

而 times[i] 相當於以節點 i 為起點，開始往其他節點擴散，求標記所有節點的最大時間成本。

試著用樹狀 dp (也就是 dfs) 求答案 times[0]。
定義 dp(i)：以節點 0 做為根，標記整個子樹 i 所需的最大成本。
轉移：dp(i) = max(dp(j) + cost)，其中 cost 根據子節點 j 的奇偶性而定。

times[0] 即為 dp(0)。

但此方法求一次答案就需要 O(N)，想要求出所有 times[i] 會高達 O(N^2)。
試著觀察不同 times[i] 之間有什麼共通點？

發現父節點 i 和子節點 j 之間，共享了 dp(j)。
有做過類似題型的話，很簡單能想到換根 dp。

示意圖

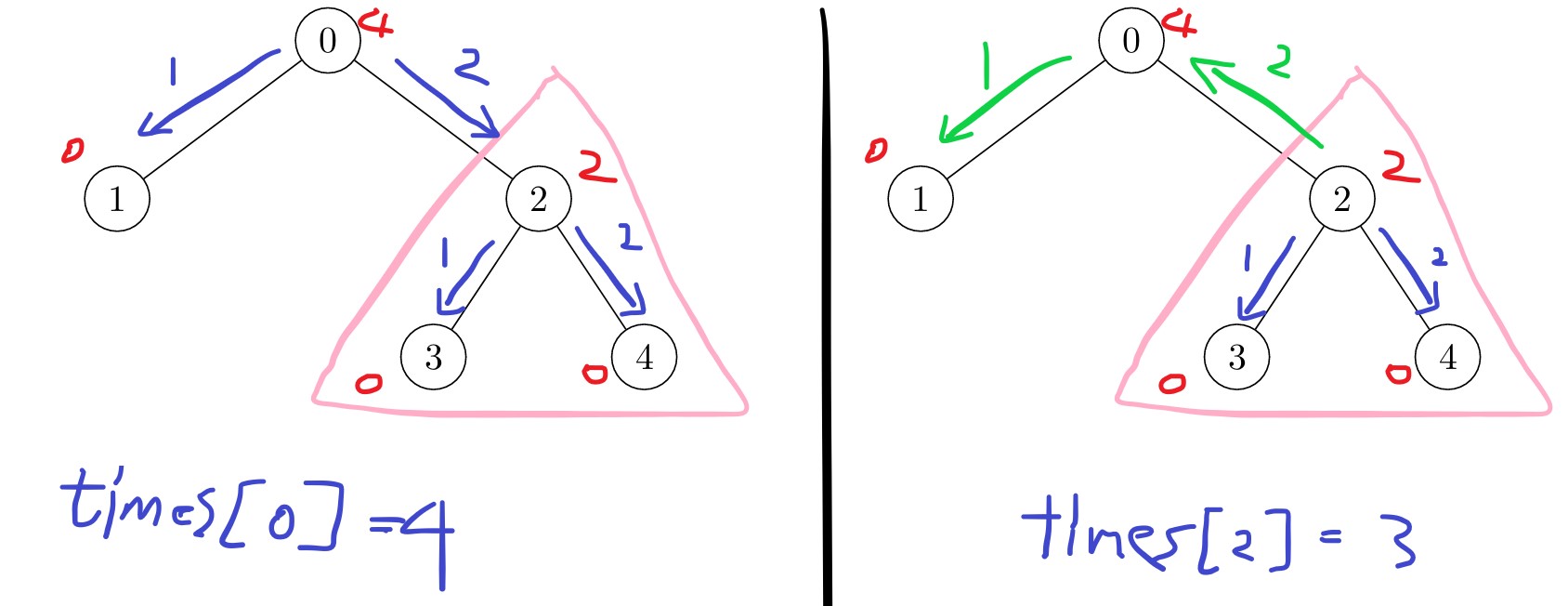
上圖以範例 3 為例，紅字為 dp(i) 的值，箭頭表示標記相鄰節點的 cost。
求 times[2] dp(2) 是標記的一部份過程，但卻不是答案。
正確答案應該是綠色，往父節點走的方向。

因此從父節點 fa 推算出子節點 i 的答案 times[i] 時，必須考慮到往父節點走的路徑最大值，記做 other。
換根後，times[i] = max(dp(i), other)。

設 i 是父節點，j 是子節點。
從 i 往 j 換根時，要找到從 j 往 i 方向標記的最大成本 other。

麻煩的點在於，在換根的時候怎麼計算往父節點的最大成本？
手上能用的東西只有 dp(i)，也就是整個子樹 i 的所需標記時間。這其中包含了 dp(j)！！
我們需要的是排除 dp(j) 的 dp(i) 值，再加上 j 往 i 走的 cost。

如果在 i 節點排除某個節點後求 dp(j) 最大值，需要 O(N)，整個複雜度又回到 O(N^2)，肯定不對。

仔細回想 dp(i) 的定義：

dp(i) = max(dp(j) + cost)

他維護的是最大的子樹標記成本。分類討論排除子樹 j 的情況：

  • 排除的 j 是成本最大的子樹，則 other = 第二大的成本 + cost
  • 排除的 j 不是成本最大的子樹，則 other = 最大的成本 + cost

只需要對於額外維護每個子樹中第二大的 dp(j) 值即可。
注意：dp(i) 維護的是整棵子樹的標記成本，判斷 dfs(j) 與 dfs(i) 兩者關係時需要額外加回 cost。

時間複雜度 O(N)。
空間複雜度 O(N)。

class Solution:
    def timeTaken(self, edges: List[List[int]]) -> List[int]:
        N = len(edges) + 1
        g = [[] for _ in range(N)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)

        dp1 = [0] * N  # max val
        dp2 = [0] * N  # second max val

        def dfs(i, fa):
            for j in g[i]:
                if j == fa:
                    continue
                cost = 1 if j & 1 else 2
                t = dfs(j, i) + cost
                if t > dp1[i]:
                    dp2[i] = dp1[i]
                    dp1[i] = t
                elif t > dp2[i]:
                    dp2[i] = t
            return dp1[i]

        dfs(0, -1)

        def dfs2(i, fa, other):
            dp1[i] = max(dp1[i], other)
            i_cost = 1 if i & 1 else 2
            for j in g[i]:
                if j == fa:
                    continue
                j_cost = 1 if j & 1 else 2
                if dp1[j] + j_cost == dp1[i]: # dp[j] is largest
                    new_other = max(other, dp2[i])
                else: # dp[j] is second largest
                    new_other = max(other, dp1[i])
                dfs2(j, i, new_other + i_cost)

        dfs2(0, -1, 0)

        return dp1