LeetCode 3240. Minimum Number of Flips to Make Binary Grid Palindromic II
biweekly contest 136。
和前一題類似,但是難度上升不少。
題目
輸入 m * n 的二進位矩陣 grid。
你可以將矩陣中任意格子的 0 翻轉成 1,或是 0 翻轉成 1。
求最少需要翻轉幾次,才能使得矩陣中所有行列都回文,且矩陣中 1 的總數必須是 4 的倍數。
解法
一開始看到 4 的倍數還覺得很奇怪,感覺沒什麼相關性。
畫個矩陣研究看看有什麼規律:
首先隨便選定一個格子,假設填了某個值。
基於列回文,同列中對稱的元素必須填入相同的值。
又基於行回文,同行中對稱的元素也必須填入相同的值。
在填完這兩格子後,他們還有還有一個共通的對稱點,也填同值。
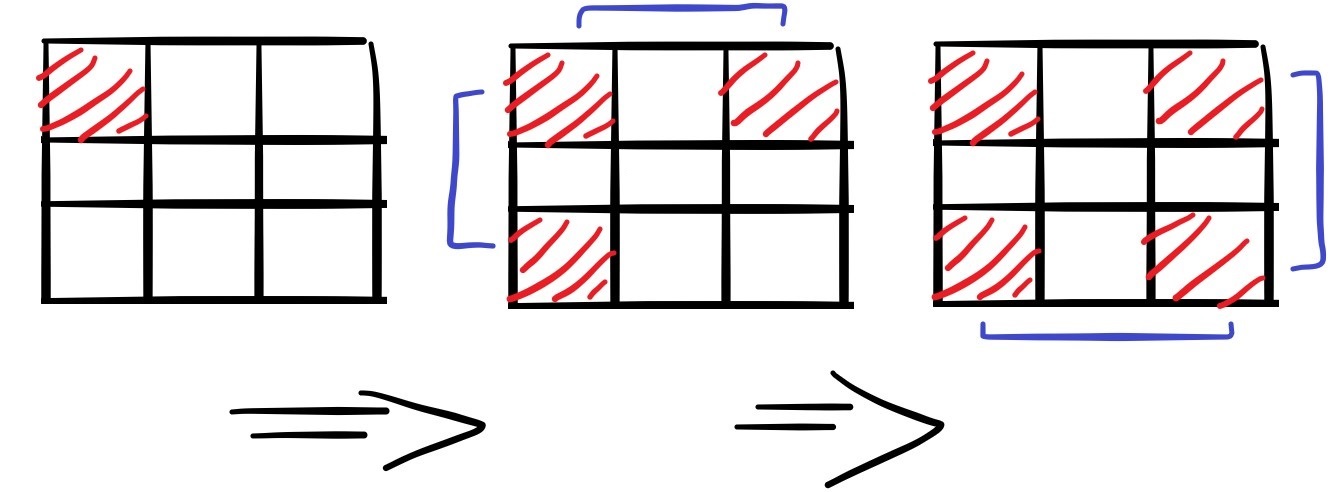
也就是說,這個四個對稱點都必須填入相同的值。
每次都是填四個 1 或 0,並不會影響 1 總數是否為 4 的倍數。
為了使修改次數最少,因此選擇修改次數較少的方案。
其餘格子同理。
回文串長度也可能是奇數。
不難看出,在行列數都是奇數時,矩陣正中心會有一個孤單的格子。
原本中心不影響回文,但本題受到 4 倍數的限制,所以必須特別把中心改成 0。
最麻煩的點在於,除了正中心以外,中間的行列也會有相同的問題。
從範例 2, 3 可以看出,在處理完四組對稱的格子後,還需額外修改才能滿足 4 的倍數。
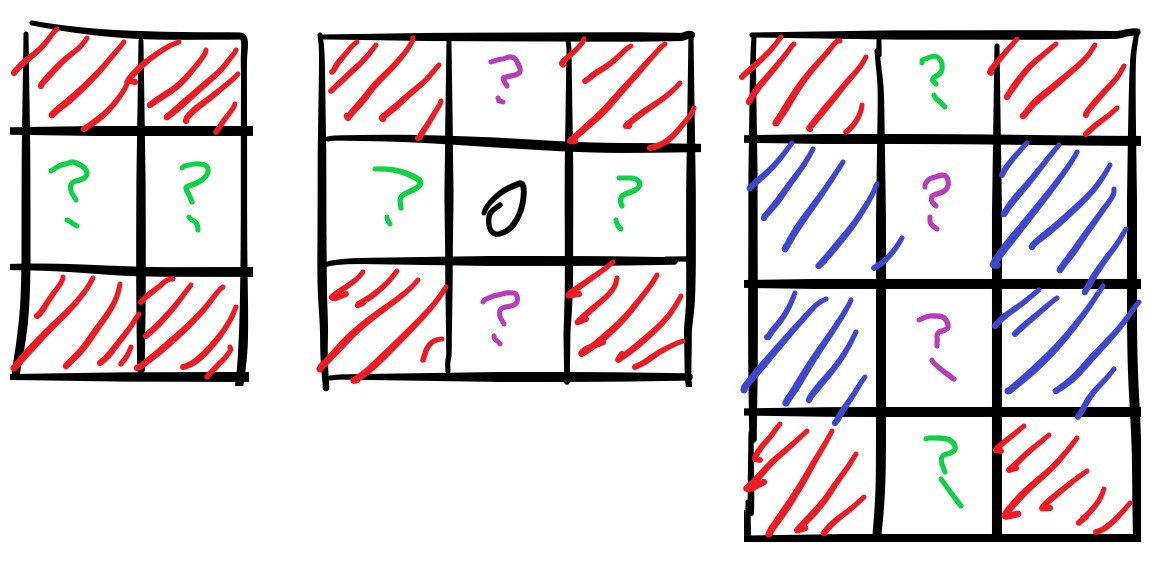
單獨判斷中間行列,回歸到最初回文兩個對稱點一組,不對稱就修改。
雖然修改其中任一都能夠滿足回文,但會影響 1 的總數。至於改成什麼先暫且不管。
至於不須修改的元素,我們還得維護現有的 1 的個數,最後才知道有沒有滿足 4 的倍數。
需要修改的組別記做 pair,現有的 1 記做 cnt1。
只有在對稱的時候才有可能增加 cnt1,所以 cnt1 必定是 2 的倍數。
而需要修改的組必定是由 0, 1 各一個組成,可以透過根據 cnt1 的值決定要改 1 還是 0。
分類討論兩種情形:
- pair > 0
- cnt1 為 4 的倍數,把 pair 組全改成 0
- cnt1 不為 4 的倍數,把一組改成 1,其餘 pair - 1 組都改成 0
- pair = 0
- cnt1 為 4 的倍數,合法
- cnt1 不為 4 的倍數,無法透過對稱組增加 1,只能把多餘的 1 單獨改成 0
時間複雜度 O(MN)。
空間複雜度 O(1)。
class Solution:
def minFlips(self, grid: List[List[int]]) -> int:
M, N = len(grid), len(grid[0])
ans = 0
for r in range(M // 2):
for c in range(N // 2):
cnt1 = grid[r][c] + grid[M-1-r][c] + grid[r][N-1-c] + grid[M-1-r][N-1-c]
ans += min(cnt1, 4 - cnt1)
if N % 2 and M % 2 and grid[M//2][N//2] == 1:
ans += 1
pair = 0
cnt1 = 0
if M % 2:
r = M // 2
for c in range(N // 2):
if grid[r][c] != grid[r][N-1-c]:
pair += 1
else:
cnt1 += grid[r][c] * 2
if N % 2:
c = N // 2
for r in range(M // 2):
if grid[r][c] != grid[M-1-r][c]:
pair += 1
else:
cnt1 += grid[r][c] * 2
if pair > 0:
ans += pair
else:
ans += cnt1 % 4
return ans