LeetCode 3235. Check if the Rectangle Corner Is Reachable

July 29, 2024

weekly contest 408。比賽當時測資範圍描述有爭議，但還是有人能猜到正解，非常厲害。

題目

輸入兩個正整數 X, Y，還有二維整數陣列 circles，其中 circles[i] = [x_i, y_i, r_i]，代表有個圓心在 (x_i 和 y_i)，其半徑為 r_i。

在座標平面上有一個矩形，其左下角位於原點，右上角位於 (X, Y)。
你必須判斷是否存在任意存在於矩形內的路徑，能夠從左下角前往右上角，途中不可接觸、穿越任何圓，並且只在兩個角落接觸矩形。

若路徑存在回傳 true，否則回傳 false。

解法

第一眼看到題目時覺得很奇怪，圓形可以覆蓋到座標平面的任何點，不僅僅是整數座標。
座標可以被無限切分，想要維護座標是否被覆蓋肯定不現實。

試想圓怎樣擺才能擋住路徑？

當矩形左下和右上角被一個 (或多個) 圓形完全隔開時，不存在任何縫隙可以通過。

因此可以判斷兩邊界是否能透過圓型連接起來，只要能連接，則不可能存在路徑。

示意圖

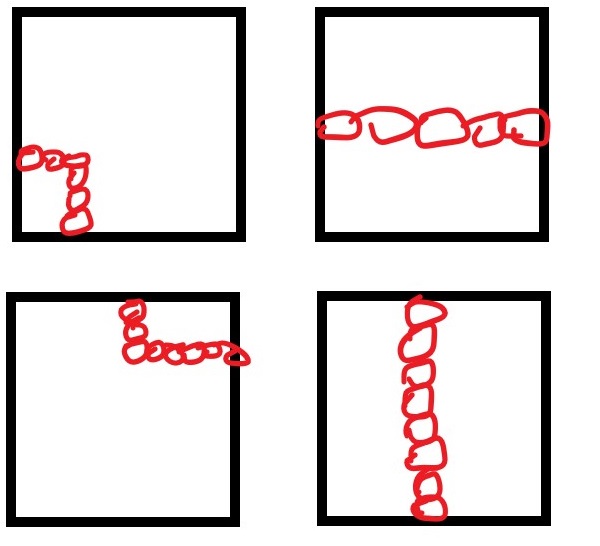
注意：本題正確的測資範圍應限制圓心位於矩形內，否則存在各種奇怪的姿勢能讓左右邊界在矩形外連通，但不阻礙矩形內路徑。
比賽當時並沒有此限制，因此存在瑕疵。現已更正。

因為要考慮兩個邊界與圓的連通性，因此使用併查集。
將 N 個圓分別編號 0 ~ N - 1，左邊界為 N，右邊界為 N + 1。

首先判斷所有圓是否接觸邊界，只要簡單的拿圓心和半徑計算即可。
再來枚舉兩個圓做一對，以勾股定理判斷兩圓心直線距離，不小於兩圓半徑和則連通。

最後判斷左右邊界是否連通即可。

時間複雜度 O(N^2 * log(N))。
空間複雜度 O(N)。

class Solution:
    def canReachCorner(self, X: int, Y: int, circles: List[List[int]]) -> bool:
        N = len(circles)
        # node 0 to N-1: circles
        # node N: left and upper bound
        # node N+1: right and lower bound
        uf = UnionFind(N + 2)

        for i, (ox1, oy1, r1) in enumerate(circles):
            # check left and upper
            if ox1 - r1 <= 0 or oy1 + r1 >= Y:
                uf.union(i, N)

            # check right and lower
            if ox1 + r1 >= X or oy1 - r1 <= 0:
                uf.union(i, N + 1)

            # check union with other circles
            for j in range(i):
                ox2, oy2, r2 = circles[j]
                # dist = sqrt((ox1 - ox2)^2 + (oy1 - oy2)^2)
                # dist <= r1 + r2 means union
                if (ox1 - ox2)**2 + (oy1 - oy2)**2 <= (r1 + r2)**2:
                    uf.union(i, j)

        return uf.find(N) != uf.find(N + 1)


class UnionFind:
    def __init__(self, n):
        self.parent = [0] * n
        for i in range(n):
            self.parent[i] = i

    def union(self, x, y):
        px = self.find(x)
        py = self.find(y)
        if px != py:
            self.parent[px] = py

    def find(self, x):
        if x != self.parent[x]:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

mocowcow

題目

解法