LeetCode 3234. Count the Number of Substrings With Dominant Ones

July 29, 2024

weekly contest 408。
想了幾天才找到滿意的做法，以前似乎沒碰過這種題型，不得不說是真的難想。
這題真的奇妙，不需要什麼特殊資料結構或是演算法，考察重點應該是觀察力，還有細節實作的細心程度。

題目

輸入二進位字串 s。

求有多少子字串是 1 顯著的。

若一個字串中 1 的數量大於等於 0 的數量的平方，則稱為 1 顯著。

解法

以下稱字串中 1 和 0 的數量為 cnt1 和 cnt2，並稱 1 顯著 為合法。
子字串合法條件為：

cnt1 >= cnt0^2

本來看到子字串問題就想要滑動窗口，但因為這個關係式比較難搞，合法的子字串不會連續出現。
例如：

s = “010111”
0 不合法
01 合法
010 不合法
0101, 01011 還是不合法
010111 突然又合法

若在 010 不合法時縮減窗口左端點，之後就算不到 010111，所以滑窗是錯的。

回頭想想最樸素的做法：暴力枚舉所有子陣列，合法就答案 +1。
這樣是 O(N^2)，對於本題 N = 4e4 來說又太多。有沒有什麼地方可以優化？

關鍵在於合法條件的公式，一個長度為 N 的合法子字串中，隱含著 N = cnt1 + cnt0^2 這個關係。代表最多只能出現 sqrt(N) 個 0！再多就不可能合法了。
如果對於 N 個左端點，分別枚舉 sqrt(N) 個 0 的右端點，複雜度 O(N sqrt(N))，計算量 8e6，看起來好多了。

現在我們要枚舉左端點 i 的子字串，然後枚舉右方至多 MX 個 0 的情形。
但如果根本沒有 0 怎麼辦？
例如：

s = “111110”
i = 0 時，cnt0 = 0，這時不管加多少 1 都合法
因此右端點的最小值為 j = 0，最大值為 k = 4
以 0 為左端點、且 cnt0 = 0 時，共有 4-0+1 個合法子字串

示意圖

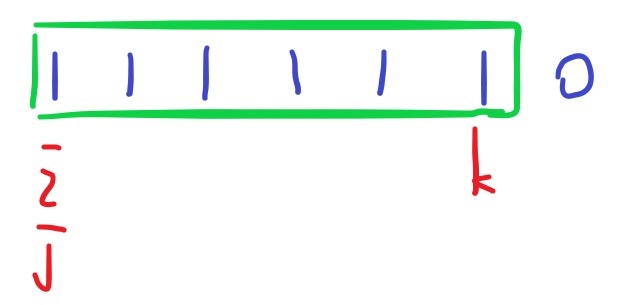
接下來正式枚舉 cnt0。
設從 i 開始向右找，找到第 cnt0 個 0 的索引為 j。
第 cnt0+1 個 0 個的前一個索引為 k。

s[i..j] 一直到 s[i..k] 的子字串中，都同樣有 cnt0 個 0。
子字串為長度 sz = j-i+1，有 sz-cnt0 個 1。
分類討論：

cnt1 >= cnt0^2：
s[i..j] 已經合法，右端點至少是 j。
cnt1 < cnt0^2：
s[i..j] 不合法，需要往後加 extra 個 1 才能變合法。
extra 至少為 cnt0^2 - cnt1。但又細分兩種情況。
- j 到 k 擁有至少 extra 個 1：
  則 s[i..j+extra] 開始合法，右端點至少是 j+extra。
- j 到 k 不足 extra 個 1：
  還是不合法，對答案無影響

示意圖

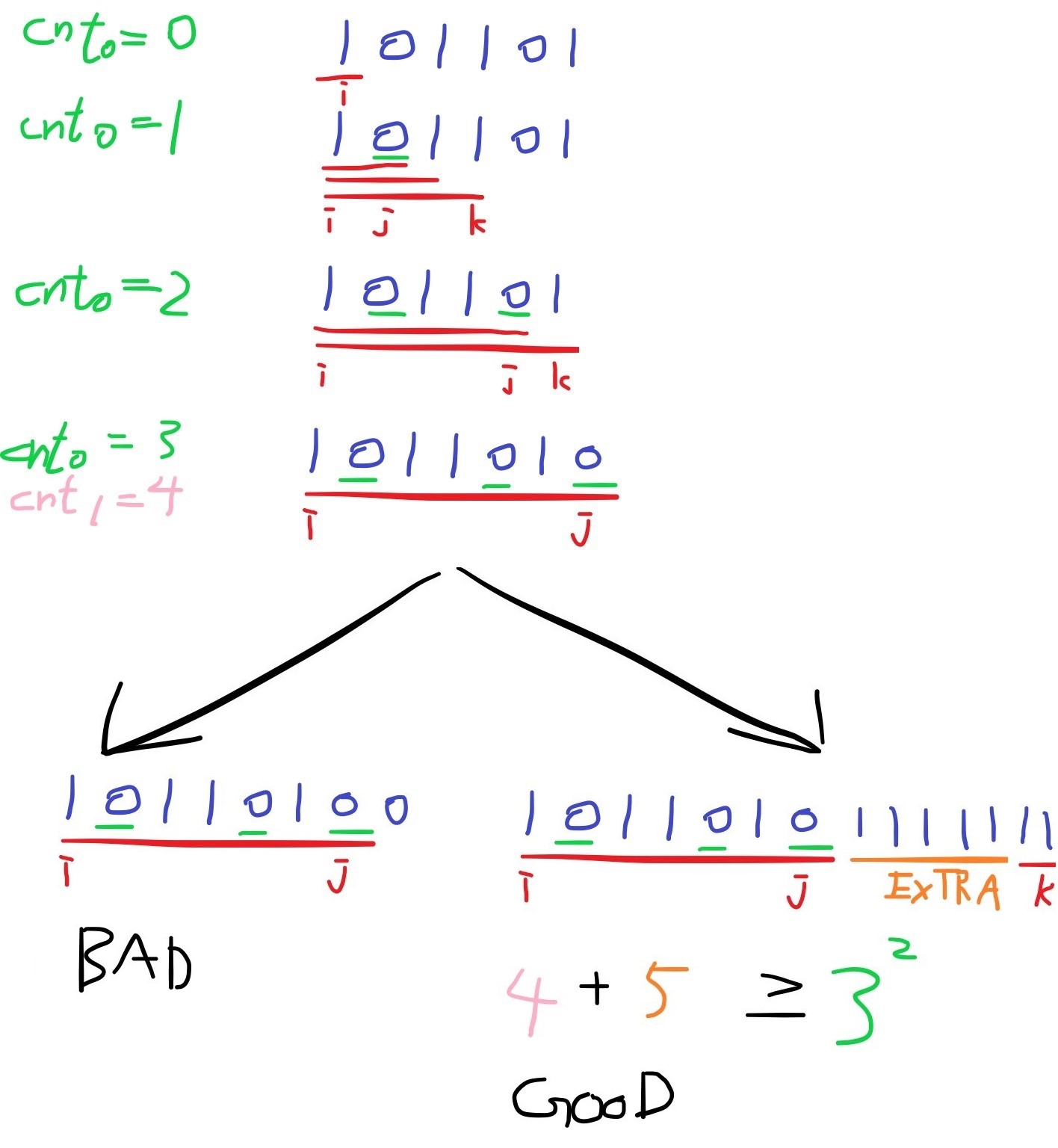
時間複雜度 O(N sqrt(N))。
空間複雜度 O(N)。

class Solution:
    def numberOfSubstrings(self, s: str) -> int:
        N = len(s)
        MX = isqrt(N)
        q = deque(i for i, c in enumerate(s) if c == "0")
        q.append(N) # sentinel
        ans = 0
        for i, c in enumerate(s):
            # substring s[i..j] only have "1"s
            if c == "1": 
                j = q[0] - 1
                ans += j - i + 1
            
            # substring s[i..j] have at least one "0"
            for zidx in range(len(q) - 1):
                j = q[zidx]
                # s[j+1..k] might have "1"s if required
                k = q[zidx + 1] - 1
                cnt0 = zidx + 1
                sz = j - i + 1
                cnt1 = sz - cnt0

                # at most MX 0s
                if cnt0 > MX:
                    break

                # case1: cnt1 >= cnt0^2
                # right bound can be [j..k]
                if cnt1 >= cnt0**2:
                    ans += k - j + 1
                
                # case2: cnt < cnt0^2
                # we need extra "1"s to make it dominant
                # right bound can be [j+extra..k]
                # cnt1 + extra >= cnt0^2
                # extra >= cnt0^2 - cnt
                else:
                    extra = cnt0**2 - cnt1
                    # ans += max(0, k - (j + extra) + 1)
                    res = k - (j + extra) + 1
                    if res > 0:
                        ans += res

            # discard expired "0"
            if c == "0":
                q.popleft()

        return ans

mocowcow

題目

解法