LeetCode 3229. Minimum Operations to Make Array Equal to Target

July 21, 2024

weekly contest 407。
原題 1526. Minimum Number of Increments on Subarrays to Form a Target Array。

題目

輸入兩個相同長度的正整數陣列 nums 和 target。

每次操作，你可以選擇任意子陣列，並且對其中所有元素都增加或減少 1。

求最少需要幾次操作，才能使得 nums 和 target 相等。

解法

首先計算出 nums 中的每個位置和 target 的差距，記做陣列 a。
a[i] = target[i] - nums[i]，代表索引 i 至少需要被增量幾次。

範例 2 很良心，告訴我們 a[i] 的值有正有負。
操作只能選擇加或減，若子陣列中同時包含正負數，肯定會造成浪費。
以 a = [1,-1] 為例：

若兩者同時加 1，會變成 [2,0]，最後 a[0] 還需要減 2 次
若兩者同時減 1，會變成 [0,2]，最後 a[1] 還需要加 2 次
最佳解是 a[0] 減 1，a[1] 加 1

由此可得知，可以分解成數個由相同正負號子陣列所組成的子問題。

將 a[i] 視作有幾顆球，則子陣列 a[i..j] 則像是由數個山形所構成。
每次操作都可以在某個高度選取連續的球，希望選擇的次數最小化。

示意圖

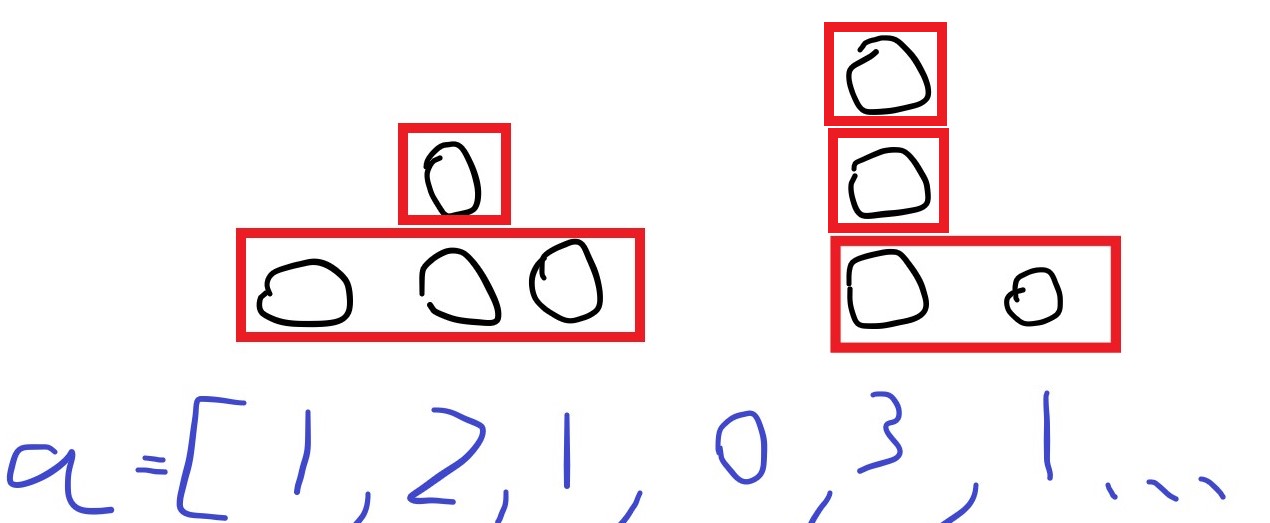
雖然畫圖來看可以很直覺找出選擇的方式，但還得想辦法用程式碼找出究竟需要選幾次。
因為選擇是橫向的，故討論 a[i] 與 a[i - 1] 在什麼情況下才能共用選擇：

若 a[i - 1] >= a[i]，很明顯可以共用所有選擇
若 a[i - 1] < a[i]，則在 a[i] 需要額外的選擇

因此對於 a[i] 點來說，所需的額外選擇次數即為 a[i] - a[i - 1]。
而 a[0] 因為沒有前者可以共用，需要直接計入次數。

注意：以上討論的都是正數的情形，實際上還要對 a[i] 取絕對值才能兼容負數情形。

時間複雜度 O(N)。
空間複雜度 O(N)。

class Solution:
    def minimumOperations(self, nums: List[int], target: List[int]) -> int:
        N = len(nums)
        a = [y - x for x, y in zip(nums, target)]

        ans = 0
        i = 0
        while i < N:
            # a[i..j] are mountains with same sign
            j = i 
            while j + 1 < N and (a[i] > 0) == (a[j + 1] > 0):
                j += 1

            # count diff
            ans += abs(a[i]) # first diff
            for k in range(i + 1, j + 1):
                ans += max(0, abs(a[k]) - abs(a[k - 1]))
            i = j + 1

        return ans

mocowcow

題目

解法