LeetCode 3224. Minimum Array Changes to Make Differences Equal

July 24, 2024

biweekly contest 135。還挺難的。
原題 1674. Minimum Moves to Make Array Complementary。

題目

輸入偶數長度 n 的整數陣列 nums，以及整數 k。

你可以對陣列進行操作，把陣列中的任意元素修改成 0 到 k 的任意整數。
你可以進行任意次操作，使得陣列滿足以下條件：

對於 0 <= i < n 的索引 i，滿足 abs(a[i] - a[n - i - 1]) = X

求滿足條件所需的最小操作次數。

解法

總共會有 n / 2 組數對 (a, b)，需要透過修改，使得他們的絕對差都變成 X。
以下為方便討論，設 a <= b。

一般直覺可能會想改成原本出現頻率最高的絕對差，但因為修改目標 [0, k] 的限制，會變成不太有效率。
例如：

k = 5
數對： (0,5), (0,5), (3,3), (3,4)

出現頻率最高的絕對差是 5。
若選擇 x = 5：

(3,3) 需要兩次操作，改成 (0,5)
(3,4) 也需要兩次操作，改成 (0,5)
共 4 次操作

若選擇 x = 0：

兩個 (0,5) 都需要一次操作，改成 (0,0) 或 (5,5)
(3,4) 需要一次操作，改成 (3,3) 或 (4,4)
共 3 次操作

可見出現頻率最高者是錯的。

既然無法直接找到最佳選項，那只好枚舉所可能的 x。

首先來研究一個滿足 a <= b 的數對 (a, b)，若要使得差值變成 x，需要如何修改：

若 b - a = x，不須修改
若 b - b != x，需要 1 或 2 次修改

但如何確認要修改幾次？
直接討論可能有點抽象，畫出出線就明瞭許多。

示意圖

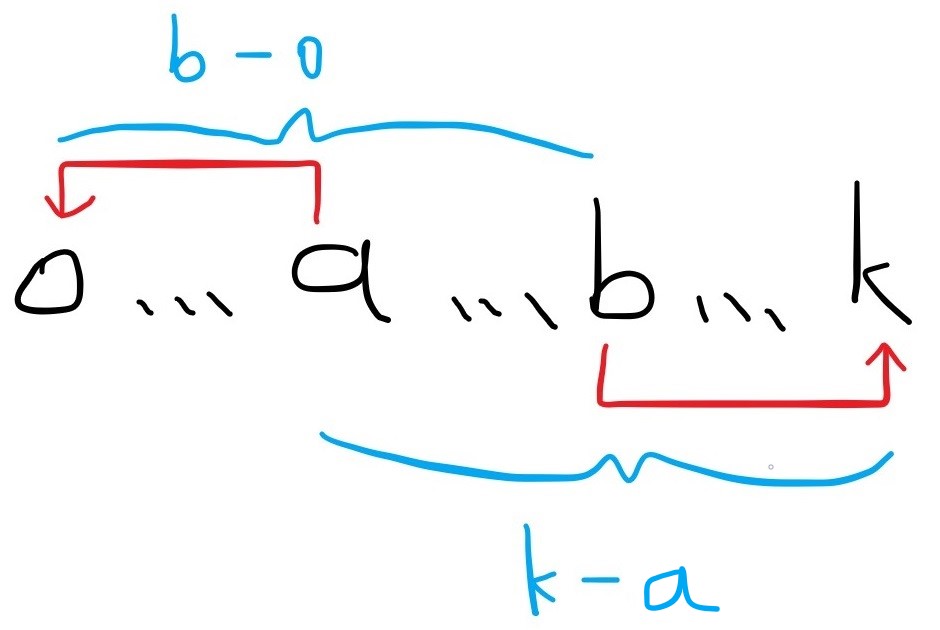
為了使 b - a 的值變大，只有兩種可能：

把 a 往左移，差變成 b - 0
把 b 往右移，差變成 k - a

兩者取最大值，就是一次操作可以調整到的最大差 mx_diff = max(b, k - a)。
若 x 大於此值，則需要第二次操作才可滿足 x。
重新整理數對 (a, b) 差值改成 x 所需修改次數：

若 x = b - a，修改 0 次
若 x <= mx_diff，修改 1 次
若 x > mx_diff，修改 2 次

設 cnt_diff[x] 為絕對差為 x 的組數，cnt_max[x] 為一次修改後至多可以變成 x 的組數。

總共有 n / 2 組數對，其中有 cnt_diff[x] 組不需修改。其餘組別至少需要 1 次，記做 first_op。
另有 cnt_max[0] + cnt_max[1] + .. + cnt_max[x - 1] 組需要額外修改第 2 次，記做 second_op。
以 first_op + second_op 即為目標差為 x 的操作次數。

但是 O(N) 暴力求 second_op 是不現實的，有幾種不同的方式供參考：

方案一：二分搜。

求出所有數對的 max_diff 後排序，可以用二分搜找到最後一個小於 x 的 max_diff 索引 idx。
從索引 0 到 idx 的所有數對都需要 2 次修改，即 second_op。

時間複雜度 O(k log n)。
空間複雜度 O(k)。

from sortedcontainers import SortedList as SL

class Solution:
    def minChanges(self, nums: List[int], k: int) -> int:
        N = len(nums)
        cnt_diff = [0] * (k + 1) # cnt diff between pair
        sl = SL() # max_diff after 1 op
        for i in range(N // 2):
            a, b = nums[i], nums[N - 1 - i]
            # keep a <= b
            if a > b: 
                a, b = b, a
                
            # [0..a..b..k]
            cnt_diff[b - a] += 1
            # option 1: move a to 0
            # diff becomes [0..b]
            # option 2: move b to k
            # diff becomes [a..k]
            sl.add(max(b, k - a))

        ans = inf
        for x in range(0, k + 1): # enumerate diff x
            no_op = cnt_diff[x]
            first_op = N // 2 - no_op

            # bisect for max_diff < x
            idx = sl.bisect_left(x) - 1 # sl[0..idx] are all < x
            second_op = idx + 1

            # update answer
            ans = min(ans, first_op + second_op)
        
        return ans

方案二：前綴和。

隨著 x 增大，組要第二次修改的組數越來越多，但每次都只需要多出一組 cnt_max[x - 1]。
因此可以先統計各 max_diff 為鍵值，統計出現次數，每次只需 O(1) 時間維護前綴和。

先更新答案後，再將 cnt_max[x] 累加至 second_op 中。

時間複雜度 O(n + k)。
空間複雜度 O(k)。

class Solution:
    def minChanges(self, nums: List[int], k: int) -> int:
        N = len(nums)
        cnt_diff = [0] * (k + 1) # cnt diff between pair
        cnt_max  = [0] * (k + 1) # cnt max diff after 1 op
        for i in range(N // 2):
            a, b = nums[i], nums[N - 1 - i]
            # keep a <= b
            if a > b: 
                a, b = b, a

            # [0..a..b..k]
            cnt_diff[b - a] += 1
            # option 1: move a to 0
            # diff becomes [0..b]
            # option 2: move b to k
            # diff becomes [a..k]
            cnt_max[max(b, k - a)] += 1

        ans = inf
        second_op = 0
        for x in range(0, k + 1): # enumerate diff x
            no_op = cnt_diff[x]
            first_op = N // 2 - no_op

            # update answer
            ans = min(ans, first_op + second_op)

            # prefix sum(cnt_max[0..x]) for next x
            second_op += cnt_max[x] 

        return ans

方案三：差分陣列。

換個角度思考，改成考慮數對 (a, b) 會對於不同的目標值 x 產生什麼影響？
同樣設 diff = b - a、max_diff = max(b, k - a)：

界於 [0..diff - 1] 的 x，操作次數加 1
界於 [diff + 1..max_diff] 的 x，操作次數加 1
界於 [max_diff + 1..k] 的 x，操作次數加 2

算出所有數對對於 x 不同值域的影響後，再對差分進行前綴和，得到正確的操作次數即可。

class Solution:
    def minChanges(self, nums: List[int], k: int) -> int:
        N = len(nums)
        d = [0] * (k + 2) # difference array
        for i in range(N // 2):
            a, b = nums[i], nums[N - 1 - i]
            # keep a <= b
            if a > b: 
                a, b = b, a

            diff = b - a 
            max_diff = max_diff = max(b, k - a)
            # [0..diff - 1] add by 1
            d[0] += 1
            d[diff] -= 1

            # [diff + 1..max_diff] add by 1
            d[diff + 1] += 1
            d[max_diff + 1] -= 1

            # [max_diff + 1..k] add by 2
            d[max_diff + 1] += 2
            # unnecessary
            # d[k + 1] -= 2 

        ans = inf
        ps = 0
        for x in range(0, k + 1):
            ps += d[x]
            ans = min(ans, ps)

        return ans
        # return min(accumulate(d[:k + 1]))

mocowcow

題目

解法