LeetCode 3203. Find Minimum Diameter After Merging Two Trees

周賽 404。

題目

有兩棵無向的樹，各有 n 和 m 個節點，編號分別為 0 到 n - 1 和 0 到 m - 1。

輸入兩個二維整數陣列 edges1 和 edges2，長度分別為 n - 1 和 m - 1。
其中 edges1[i] = [a_i, b_i]，代表第一棵樹中的節點 a_i 和 b_i 之間存在一條邊。
edges2 同理。

你必須將兩棵樹中各選擇一個節點並相連合併。

求合併後的樹的最小直徑。

直徑指的是一棵樹中任意兩點的最大距離。

解法

相似題 543. diameter of binary tree。
要先會求單一棵樹的直徑之後才能繼續討論。

---

以下簡稱兩棵樹為 A, B。
設 A, B 的直徑為 d1, d2。

兩樹新增一條連接邊後，原本各自的路徑會相互組成好幾條新的路徑。
怎樣選連接點才能使的產生的路徑較短？

直徑的定義，是由樹中相距最遠的兩個點組成的路徑。
而合併之後最有可能經由直徑產生更長的新路徑。
為了減少其貢獻，選擇其中點作為兩樹連接點，可使得新路徑最小化。

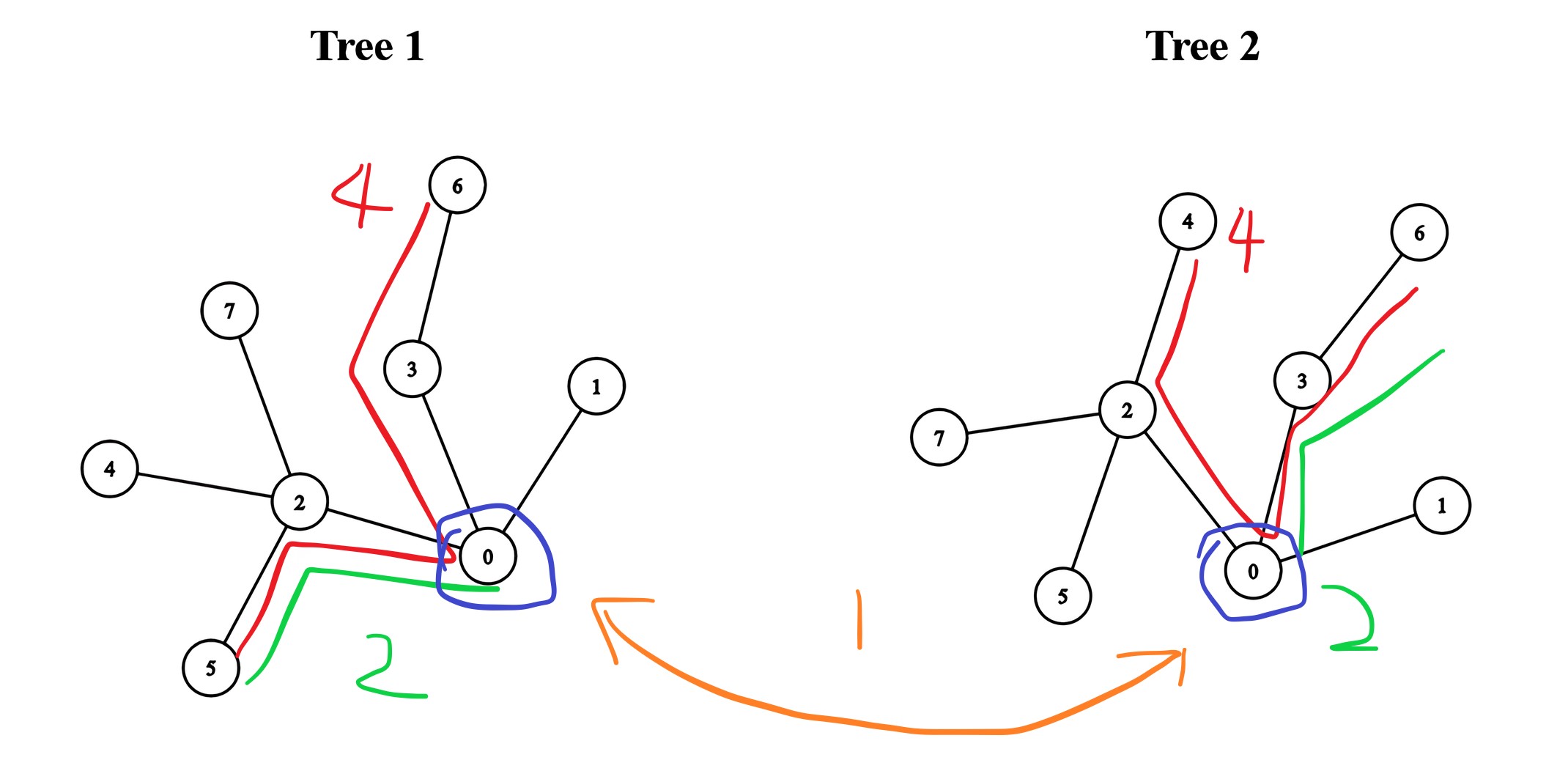
各取 A, B 直徑的一半，加上連接邊的長度 1 即為最長新路徑長度。
考慮到長度奇偶性，除二時需要向上取整。

(d1 + 1) / 2 + (d2 + 1) / 2 + 1

---

但是新路徑不一定會是最長的。舉個反例：

A 是一條長度 100 的直線，B 只是長度 4 的直線
新的最長路徑是 50 + 2 + 1

新路徑比原本的直徑還小，故正確答案需和原本的直徑取最大值。

class Solution:
    def minimumDiameterAfterMerge(self, edges1: List[List[int]], edges2: List[List[int]]) -> int:
        d1 = self.diameter(edges1)
        d2 = self.diameter(edges2)
        d3 = (d1 + 1) // 2 + (d2 + 1) // 2 + 1
        return max(d1, d2, d3)
    
    def diameter(self, edges):
        N = len(edges) + 1
        g = [[] for _ in range(N)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
            
        res = 0 
        def dfs(i, fa):
            nonlocal res
            mx1 = mx2 = 0
            for j in g[i]:
                if j == fa:
                    continue
                t = dfs(j, i)
                if t > mx1:
                    mx1, mx2 = t, mx1
                elif t > mx2:
                    mx2 = t
                    
            res = max(res, mx1 + mx2)
            return mx1 + 1
        
        dfs(0, -1)
        return res