LeetCode 32. Longest Valid Parentheses

May 24, 2022

每日題。stack的經典題，有碰到括號的題目幾乎都能用stack解決。

題目

輸入只有包含’(‘和’)’的字串，求最長的合法括號子字串的長度。

解法

合法的括號必須要由’(‘和’)’各一個所組成，再多的’(‘也不會影響答案，一定要在出現’)’時才有可能增加合法長度。

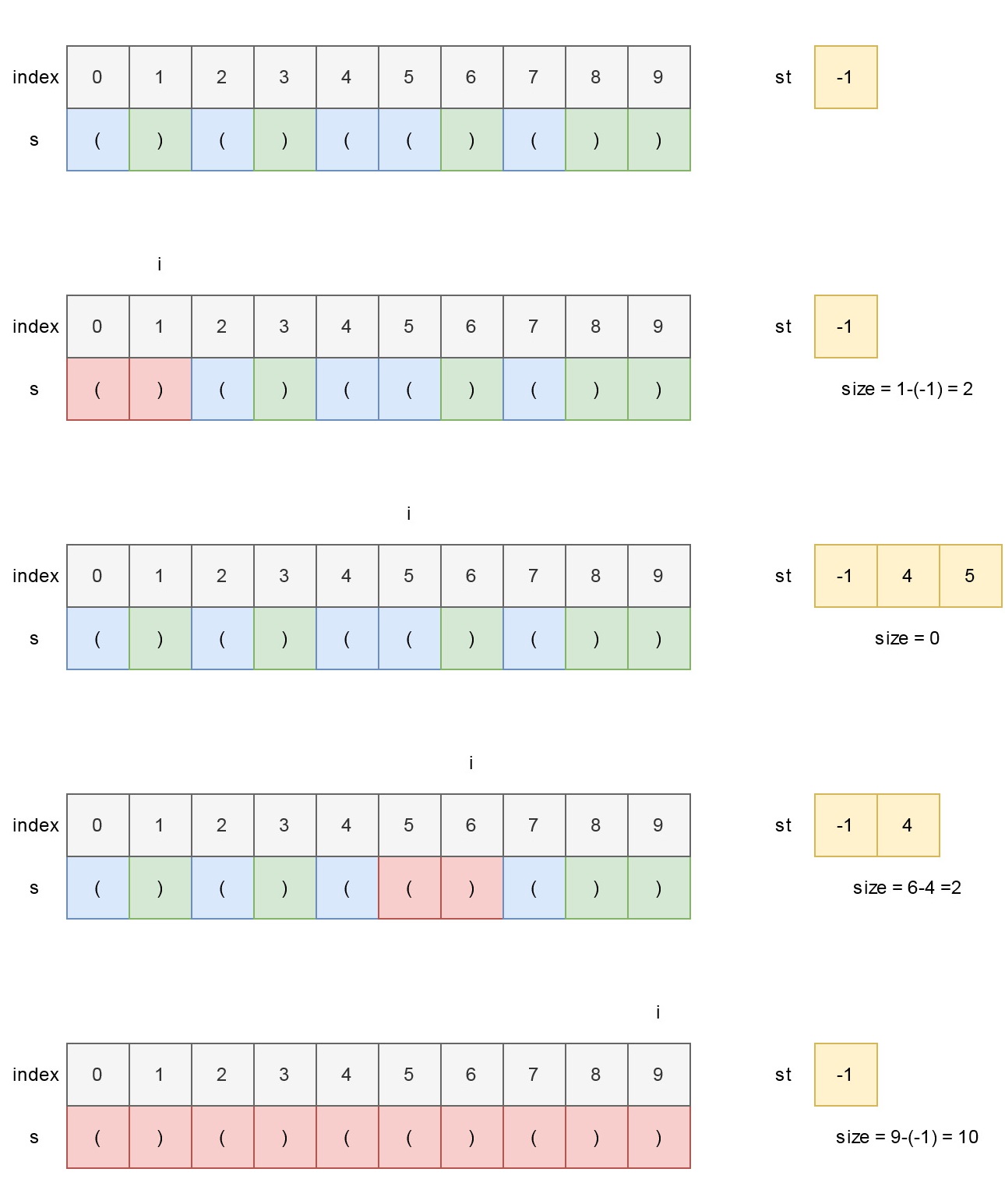
維護堆疊st，初始化放一個-1，作為有效括號子字串的起點。
遍歷每個字元s[i]，若s[i]是左括號，則將i押入堆疊中。
若s[i]是右括號，有兩種可能：

st中有許多左括號，去掉頂端的那個，並計算有效括號字串長度
st中沒有左括號，所以把子字串起點更新為i

因為我們碰到左括號時，每次都會將其索引押入st中，所以只有在左括號數量小於右括號數量時，st才會為空。這時只要將i放回st中，就可以字串更新起點。

示意圖

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        st=[-1]
        ans=0
        for i,c in enumerate(s):
            if c=='(':
                st.append(i)
            else:
                st.pop()
                if not st:
                    st.append(i)
                else:
                    ans=max(ans,i-st[-1])
                    
        return ans

看到有人用dp解法，來學習一下。
定義dp[i]：代表以s[i]結尾的最常有效括號字串長度。

左括號不可能結尾，所以s[i]為左括號時dp[i]一定是0。
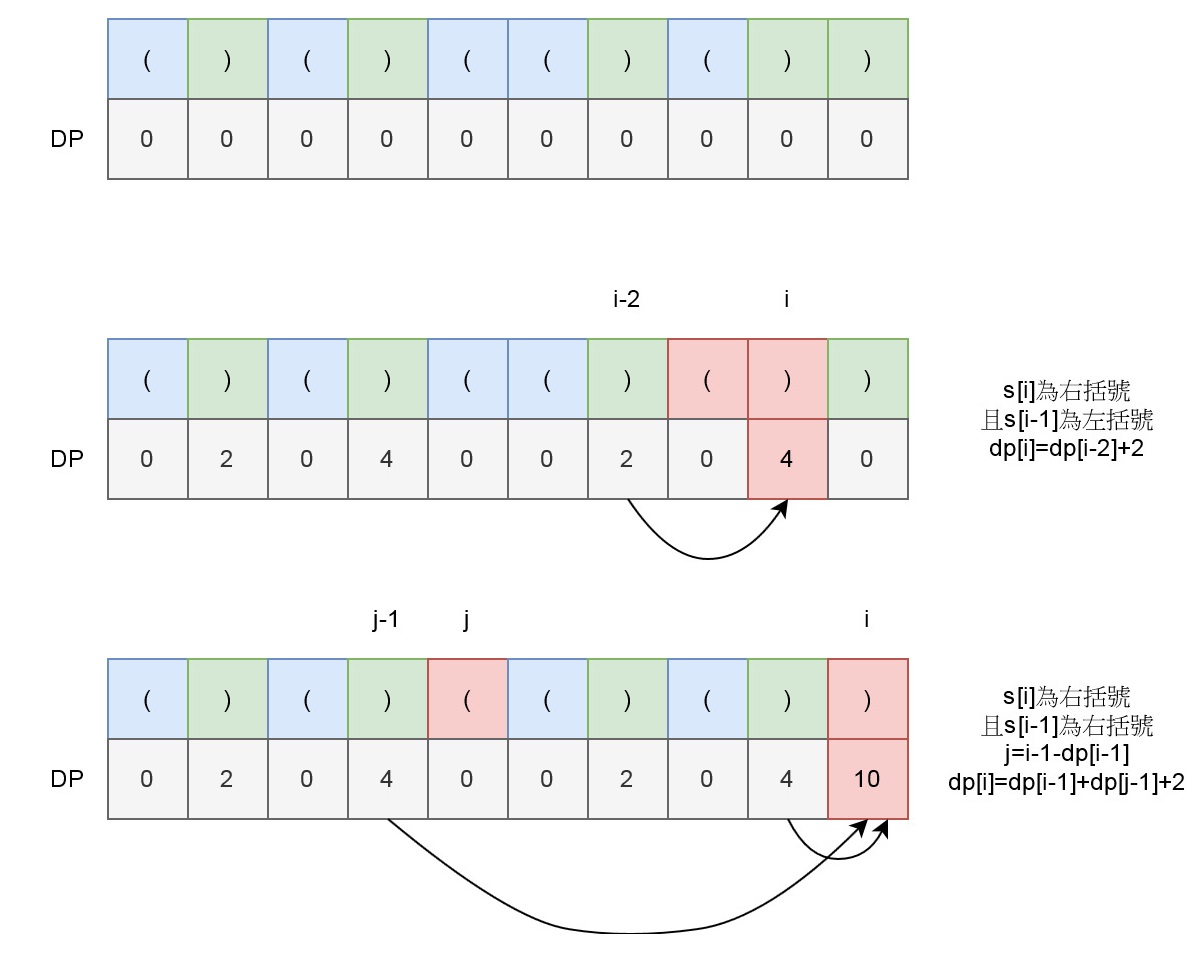
s[i]是右括號時，有兩種狀況：

s[i-1]是左括號，剛好形成一對，所以dp[i]=dp[i-2]+2
s[i-1]是右括號，那就要根據dp[i-1]來找到上一個位置j，j=i-1-dp[i-1]，若j大於等於0且s[j]正好是左括號，則dp[i]=dp[i-1]+dp[j-1]+2

示意圖

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        if not s:
            return 0
        
        N=len(s)
        dp=[0]*N
        for i in range(1,N):
            if s[i]==')':
                if s[i-1]=='(':
                    dp[i]=dp[i-2]+2
                else:
                    j=i-1-dp[i-1]
                    if j>=0 and s[j]=='(':
                        dp[i]=dp[i-1]+dp[j-1]+2
                        
        return max(dp)

mocowcow

題目

解法