LeetCode 3197. Find the Minimum Area to Cover All Ones II
周賽 403。 完全沒有頭緒怎麼搞。就算後來知道思路後還是很難寫,非常吃細節。
題目
輸入二維二進位陣列 grid。
你必須找到三個不重疊、且面積不為 0 的矩形,並確保這三個矩形包含矩陣中所有的 1。
求三個矩形的最小可能總面積。
注意:矩形的邊界允許相交。
解法
個人認為,這題的難點在於想到重複利用之前 Q2 的解法,把原本的矩形切兩刀、變成三塊,變成三個同樣的子問題。
如果沒想通這點,則很容易糾結如何找到三個剛好、無多餘的矩形,因此無法分析出正確的切割方式。
先想想如果要分成兩塊,有兩種切法。
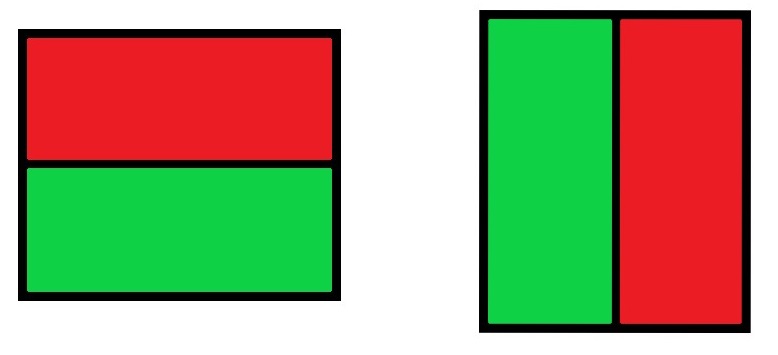
然後從不同顏色的區域中分別以 Q2 的方式求出最小所需面積。
如果要分成三塊,則有六種切法。
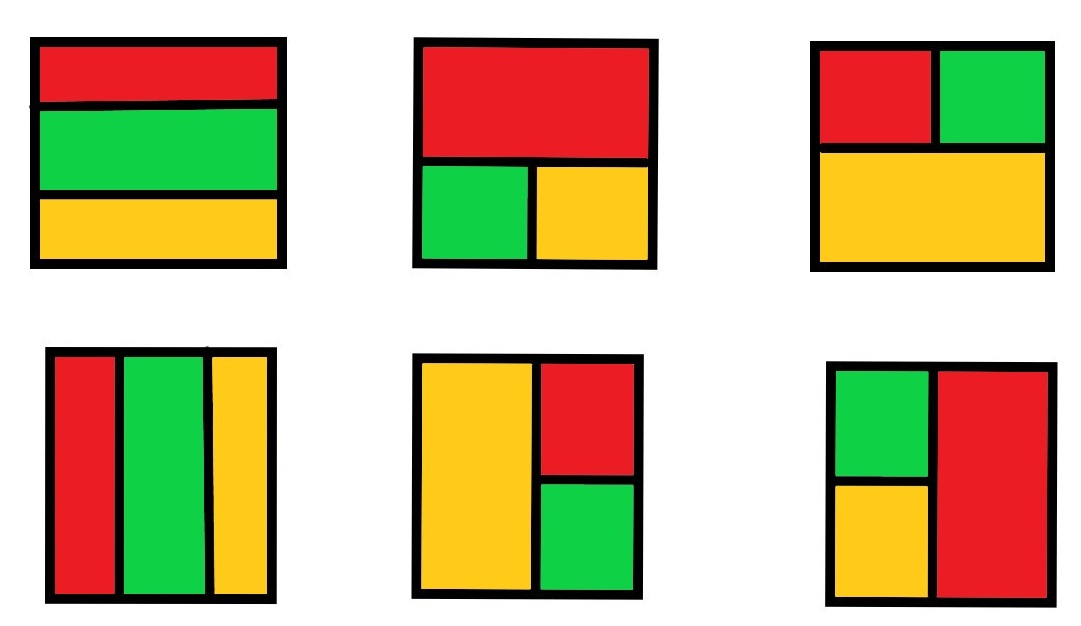
對於本題來說,只需要暴力枚舉 6 種切法中,切在不同行列上的結果,並找到最小值即可。
雖然說是寫暴力法,但其實可以不必考慮某些細節,寫起來會比較省力。
首先是關於空矩形。
雖然題目要求分割後的矩形面積至少為 1,但就算某個部分是空的,也不會影響答案,不用過度考慮邊界。
再來是不同切法中的共通點。
除了三橫和三直以外的四種 T 型切法,其實都是依賴於一個十字型分割線,不過只有其中一半要切第二刀。
這樣就可以把四個雙迴圈濃縮成一個,輕鬆不少。
時間複雜度 O((nm) ^ 2)。
空間複雜度 O(1)。
class Solution:
def minimumSum(self, grid: List[List[int]]) -> int:
M, N = len(grid), len(grid[0])
@cache
def f(r1, r2, c1, c2):
up = inf
down = -inf
left = inf
right = -inf
for r in range(r1, r2 + 1):
for c in range(c1, c2 + 1):
if grid[r][c] == 1:
up = min(up, r)
down = max(down, r)
left = min(left, c)
right = max(right, c)
w = right - left + 1
h = down - up + 1
return w * h
ans = inf
# 3 horizon
for i in range(M):
for ii in range(i + 1, M):
a1 = f(0, i, 0, N - 1)
a2 = f(i + 1, ii, 0, N - 1)
a3 = f(ii + 1, M - 1, 0, N - 1)
ans = min(ans, a1 + a2 + a3)
# 3 vertical
for j in range(N):
for jj in range(j + 1, N):
a1 = f(0, M - 1, 0, j)
a2 = f(0, M - 1, j + 1, jj)
a3 = f(0, M - 1, jj + 1, N - 1)
ans = min(ans, a1 + a2 + a3)
# 4 type of T-shapes splited by a cross
for i in range(M):
for j in range(N):
# 1 top + 2 down
a1 = f(0, i, 0, N - 1)
a2 = f(i + 1, M - 1, 0, j)
a3 = f(i + 1, M - 1, j + 1, N - 1)
ans = min(ans, a1 + a2 + a3)
# 2 top + 1 down
a1 = f(0, i, 0, j)
a2 = f(0, i, j + 1, N - 1)
a3 = f(i + 1, M - 1, 0, N-1)
ans = min(ans, a1 + a2 + a3)
# 1 left + 2 right
a1 = f(0, M - 1, 0, j)
a2 = f(0, i, j + 1, N - 1)
a3 = f(i + 1, M-1, j + 1, N-1)
ans = min(ans, a1 + a2 + a3)
# 2 left + 1 right
a1 = f(0, i, 0, j)
a2 = f(i + 1, M - 1, 0, j)
a3 = f(0, M - 1, j + 1, N - 1)
ans = min(ans, a1 + a2 + a3)
return ans