LeetCode 3179. Find the N-th Value After K Seconds

周賽 401。

題目

輸入兩個整數 n 和 k。

最初，你擁有一個長度為 n 的陣列 a，初始值都是 1。
之後每一秒，你需要同時更新陣列中所有 a[i] 的值為其前方的所有元素和，再加上自己。
例如：經過一秒後，a[0] 維持不變；而 a[1] 變成 a[0] + a[1]；而 a[2] 變成 a[0] + a[1] + a[2]。以此類推。

求 k 秒後 a[n - 1] 的值。
答案可能很大，先模 10^9 + 7 後回傳。

解法

更新操作其實就是前綴和。
按照題意模擬，對 a 求前綴和 k 次即可。

時間複雜度 O(nk)。
空間複雜度 O(n)。

MOD = 10 ** 9 + 7
class Solution:
    def valueAfterKSeconds(self, n: int, k: int) -> int:
        a = [1] * n
        for _ in range(k):
            a2 = []
            ps = 0
            for x in a:
                ps += x
                ps %= MOD
                a2.append(ps)
                
            a = a2
            
        return a[-1]

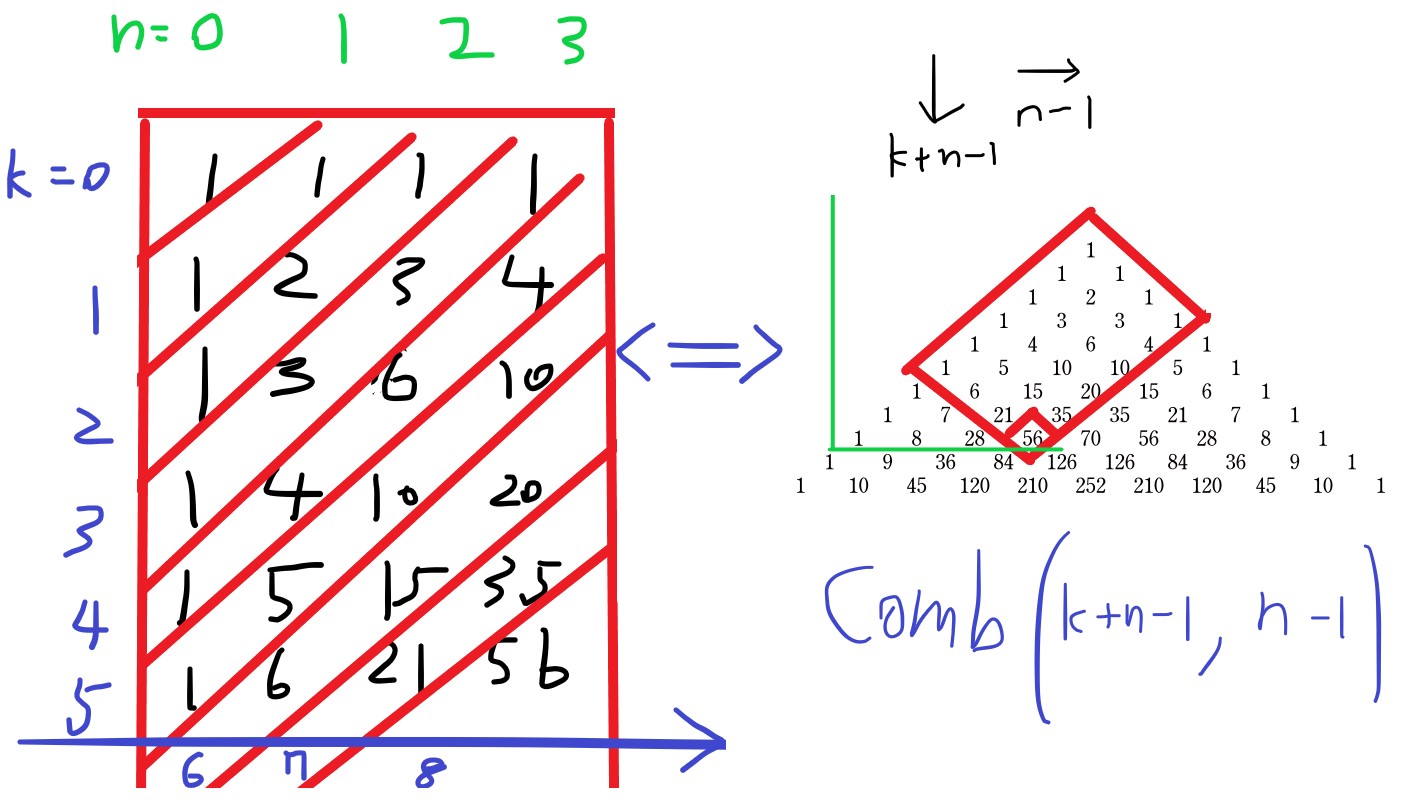
定睛一看，發現這個規律好像有點眼熟。
如果把頭往左側轉 45 度一看，原來是巴斯卡三角形。

巴斯卡三角形等價於組合數。
觀察下圖規律，推算出答案目標位於第 k + n - 1 列、第 n - 1 個行，答案就是 comb(k+n-1, n-1)。

時間複雜度 O(1)，預處理時間不計。
空間複雜度 O(1)。

MOD = 10 ** 9 + 7
class Solution:
    def valueAfterKSeconds(self, n: int, k: int) -> int:
        return comb(k+n-1, n-1) % MOD

其他語言比較麻煩，需要自己預處理階乘和乘法逆元。
以下是 golang 範例。

const MX = 2000
const MOD int = 1e9 + 7
var f, finv [MX + 1]int

func init() {
    f[0], finv[0] = 1, 1
    f[1], finv[1] = 1, 1
    for i := 2; i <= MX; i++ {
        f[i] = f[i-1] * i % MOD
        finv[i] = fast_pow(f[i], MOD-2, MOD)
    }
}

func fast_pow(base, exp, MOD int) int {
    res := 1
    for exp > 0 {
        if exp%2 == 1 {
            res = res * base % MOD
        }
        base = base * base % MOD
        exp >>= 1
    }
    return res
}

func valueAfterKSeconds(n int, k int) int {
    return f[k+n-1] * finv[n-1] % MOD * finv[k] % MOD
}