LeetCode 304. Range Sum Query 2D - Immutable

可怕的2D前綴和。原來以前我是偷工減料過關的，沒有學會其中精華，今天特地來補課。

題目

設計一個類別NumMatrix，包含以下功能：

• 建構子，傳入二維矩陣初始化
• int sumRegion(r1,c1,r2,c2)，以(r1,c1)為左上角，(r2,c2)為右下角，回傳矩形內的數值總和

解法

先複習偷工減料版本。
對每個row做前綴和而已，實際上查詢的時候還是要對M個row求值。
每次查詢時間為O(M)，初始化時間為O(M*N)。

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        M,N=len(matrix),len(matrix[0])
        self.psum=[[0]*(N+1) for _ in range(M)]
        for r in range(M):
            for c in range(N):
                self.psum[r][c+1]=self.psum[r][c]+matrix[r][c]
    
    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        ans=0
        for r in range(row1,row2+1):
            ans+=self.psum[r][col2+1]-self.psum[r][col1]
        return ans

更佳解法應該是做2D的前綴和，保存原點到某個點的範圍加總。
查詢時間為O(1)，初始化時間為O(M*N)。

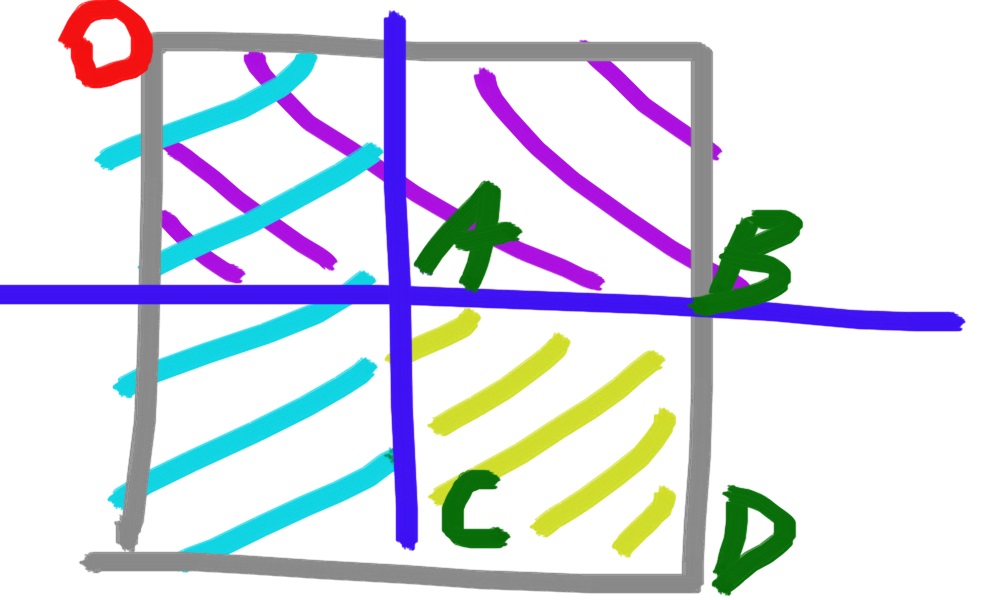
建立OD時，由公式推出：OD=OB+OC-OA+matrix[i][j]
查詢AD，由公式推出：AD=OD-OB-OC+OA

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        M,N=len(matrix),len(matrix[0])
        self.psum=[[0]*(N+1) for _ in range(M+1)]
        for r in range(M):
            for c in range(N):
                self.psum[r+1][c+1]=self.psum[r][c+1]+self.psum[r+1][c]-self.psum[r][c]+matrix[r][c]

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return self.psum[row2+1][col2+1]-self.psum[row2+1][col1]-self.psum[row1][col2+1]+self.psum[row1][col1]