LeetCode 3025. Find the Number of Ways to Place People I

February 4, 2024

雙周賽123。有點油的題目，可能是因為 Alice 和 Bob 出現太多次，這次主角變成動畫人物了。

題目

輸入 x * 2 的二維陣列 points，代表平面上的某些點的整數座標點，其中 poins[i] = [x_i, y_i]。

定義右方為 x 軸的方向，而左方為 x 軸的反方向；同理，上方為 y 軸方向，下方為 y 軸反方向。

你必須安排包千束和瀧奈在內，共 n 個人的位置，每個點只能站一個人。
千束想和瀧奈獨處，所以千束會建立一個矩形的柵欄，以自身為左上角，且瀧奈為右下角。柵欄不一定是矩形，也可能只是一條線。
如果柵欄的範圍內中有其他人在，千束會很難過。

求有幾組座標數對能夠分別放置千束和瀧奈，且不讓千束感到難過。

解法

在測資不大的情況下，暴力法是可行的。

枚舉所有數對 (i, j)，其中 i 是左上角，j 是右下角。
判斷 i, j 之間的上下關係之後，再枚舉所有點 k，若沒有電燈泡在裡面，則答案加 1。

時間複雜度 O(n^3)。
空間複雜度 O(1)。

class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        ans = 0
        for i, (x1, y1) in enumerate(points):
            for j, (x2, y2) in enumerate(points):
                if i == j:
                    continue
                
                if not (x1 <= x2 and y1 >= y2):
                    continue
                
                for k, (x3, y3) in enumerate(points):
                    if k == i or k == j:
                        continue
                    if x1 <= x3 <= x2 and y1 >= y3 >= y2:
                        break
                else:
                    ans += 1
                    
        return ans

在 Q4 的時候，points 大小上升到 1000，暴力法肯定是不行了。
在枚舉 (i, j) 的過程中，想想有沒有辦法優化找中間點的過程。

我在比賽中想到的是二維前綴和，直接以 i 為左上角，j 為右下角，若範圍內只有 2 個點，則代表沒有電燈泡。
但是細節出了點問題，沒做出來，之後在找時間補寫。

來個更簡單的做法。

若我們固定一個點 j 作為右下角，其座標為 (x2, y2)，並且要枚舉點 i 作為左上角，按照怎樣的順序比較合理？
肯定是從 x2 - 1 開始向左邊找。因為 x1 越靠近 x2，中間包含其他電燈泡的機率就越小。

那如果同個 x 軸上，有數個點分布在不同 y 軸，那又如何？
其實只有 y 軸最小的那個點有機會，因為搭配更大的 y，也一定會框到最底下那個。

繼續往更小的 x 軸找，後來的點也都會受限於之前點的 y 軸。也就是說，越往左走，能框的 y 軸會嚴格遞減。
如下圖：
示意圖

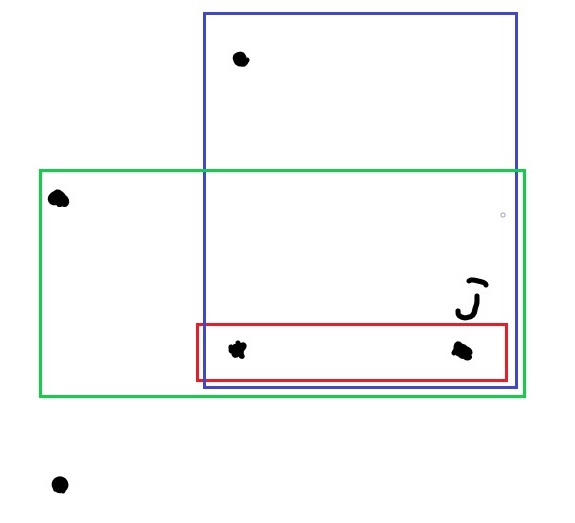
藍框和紅框的 x 的是相同的，但是只能選擇 y 軸較小的紅框
接下來考慮綠框。但綠框的 y 軸高於紅框，必定不合法
綠框下面那個點更不用說了，甚至比 j 點的 x 軸還小，完全不考慮
答案只有紅框 1 種

再來看看圖二：
示意圖

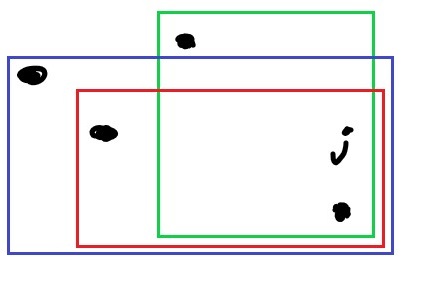
綠框合法紅框也比綠框低，合法
藍框比紅框高，不合法答案有綠框和紅框 2 種

為了能夠按照上述方式遍歷每個點，則需要將 points 偏序排序。先以 x 軸遞增，若 x 軸相同再以 y 軸遞減。

對於固定的右下角 j，其 y 軸為 y2，從右往左枚舉左上角 i，其 y 軸為 y1，並維護 y 軸最高合法高度 y_limit。
若 y1 軸不小於 y2，且小於 y_limit，則答案加 1，並更新 y_limit。

時間複雜度 O(N^2)。
空間複雜度 O(1)。

class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        points.sort(key=lambda x: (x[0], -x[1])) 
        ans = 0
        for j, (_, y2) in enumerate(points):
            y_limit = inf
            for i in reversed(range(j)): # (i, j)
                y1 = points[i][1]
                if y1 >= y2 and y1 < y_limit:
                    y_limit = y1
                    ans += 1
                
        return ans

有些朋友可能覺得從右下角往左上角框出一個矩形很不舒服，因此提供左上往右下框的版本。
邏輯大致相同，只是改成固定左上角，向右枚舉右下角，並且右下角的 y 軸高度變成嚴格遞增。

class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        N = len(points)
        points.sort(key=lambda x: (x[0], -x[1])) 
        ans = 0
        for i, (_, y1) in enumerate(points):
            y_limit = -inf
            for j in range(i+1, N):
                y2 = points[j][1]
                if y1 >= y2 and y2 > y_limit:
                    ans += 1
                    y_limit = y2
                
        return ans

mocowcow

題目

解法