LeetCode 2983. Palindrome Rearrangement Queries

January 4, 2024

周賽378。有夠臭長的模擬題，非常多細節要考慮。
雖然說不需要什麼高級的DSA，但要在一小時內寫出來還挺難的，我用python也寫了一小時多。

題目

輸入長度n的字串s。

另外輸入二維整數陣列queries，其中queries[i] = [a_i, b_i, c_i, d_i]。

對於每個查詢i，你必須執行以下操作：

將子字串s[a_i:b_i]中的字元重新排序。保證0 <= a_i <= b_i < n / 2。
將子字串s[c_i:d_i]中的字元重新排序。保證n / 2 <= c_i <= d_i < n。

你的目標是透過重排序子字串，使得s成為一個回文字串。

每次查詢都是獨立的，重排序的結果都會被重置。
回傳陣列answer，若第i次查詢可以得到回文字串，則answer[i]=true；否則為false。

注意：此處s[x:y]為閉區間，子字串包含x,y兩個端點。

解法

先看測資限制，保證s是偶數，且a,b只會在左半邊、而c,d只會在右半邊。

回文的定義是：從左到右讀起來與從右到左的結果相同。
可以把回文拆成兩半，左半會等於反轉過的右半。
將左半記做s1，反轉過的右半記做s2。
例如：s=”abba, s1=”ab”，s2=”ab”。

示意圖

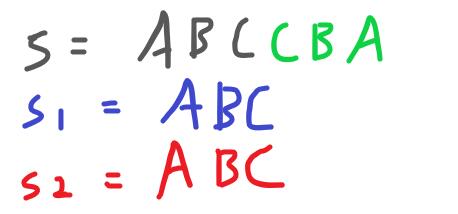
反轉了s2，所以查詢範圍[c, d]也要記得一起反轉。
查詢的要求轉換為：

重排序s1[a:b]
重排序s2[c:d]
判斷s1是否等於s2

最特殊的例子是反轉範圍覆蓋整個字串，任意重排整個s1和s2。
只要兩者的字元出現次數相同，則可以重排成相同結果；反之則不可能。

繼續分類討論兩個反轉區間的關係。方便起見，將s1的反轉區間記做[L1, R1]，而s2的區間記做[L2, R2]，並限制L1 <= L2。
有三種情形：

無交集
某區間被另一個區間包含
部分交集

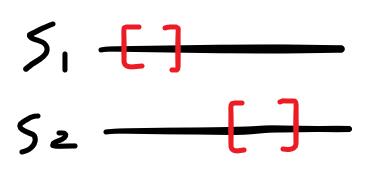
無交集時，s1[L1, R1]可以重排，但必須和s2[L1, R1]的字元計數相等。[L2, R2]的部分同理。
但因為無交集，[R1, L2]之間可能存在不能重排的部分，這段區間的子字串必須相等。L1左方與R2右方同理。

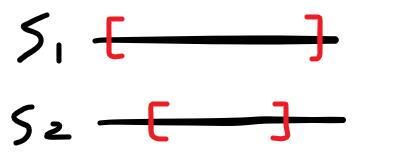
區間被包含時，[L1, R2]覆蓋整個[L2, R2]。其實一個區間內只要至少一個字串能重排，那就有機會排成相同的字串。只要檢查s1和s2的[L1, R2]字元計數是否相等。
記得L1左方和R1右方不能重排，子字串必須相等。

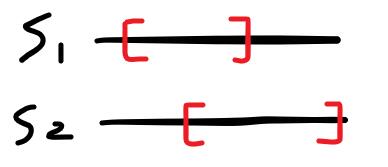
部分交集，這個情況比較難想。
s2的[R1, L2-1]這部分不能動，需要靠移動s1來達成相等。先從s1的[L1, R1]這部分拿出需要的字元換過去。
s1的[R1+1, L2]也不能動，只能移動s2的[L2, R2]字元移過去。
當然，可移動的字元有時根本就不夠，那就沒辦法完成；如果夠，剩下的字元才排在交集的部分。
別忘了最左和最右方都有一區不能動的，他們必須相等。

剛才只講了L1 <= L2的情形，但其實兩者是對稱的。
如果碰到L1 > L2時，直接將兩者互換即可。

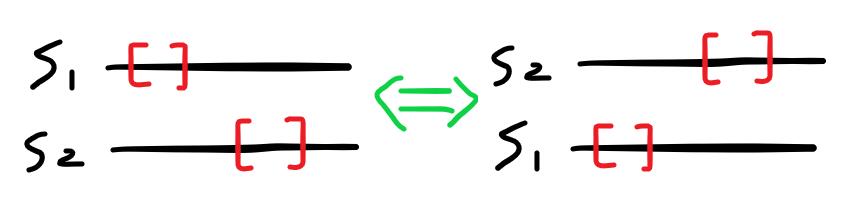
剛才分類的三種情形都有共通點：檢查最左和最右不可重排的子字串。可以提取出來統一處理。

目前為止，我們需要查詢字串某個區間中各字元出現次數。
只需要區間查詢，不需要修改，首選當然是前綴和。

然後還要判斷兩字串某個區間是否完全相等。
有點難想，但其實也是前綴和求s1[i] != s2[i]的次數，若為0則代表完全相同。

把查詢中會多次查詢前綴和、甚至對前綴和做減法，把這些重複的邏輯抽象成函數：

get_ps() 求字串區間前綴和
get_diff() 求s1, s2區間不同字元數
can_swap() 求s2, s2區間中字元出現次數是否相等
subtract() 對兩個字元前綴和做減法，若出現負數則回傳空陣列

自上而下將邏輯實現即可。

時間複雜度O(N + Q)，N為s長度，Q為查詢次數。
空間複雜度O(N)。

class Solution:
    def canMakePalindromeQueries(self, s: str, queries: List[List[int]]) -> List[bool]:
        N=len(s)
        size=N//2
        s=[ord(c)-97 for c in s]
        s1=s[:size]
        s2=s[size:][::-1]
        
        # pruning
        if Counter(s1)!=Counter(s2):
            return [False]*len(queries)

        # prefix sum for 26 chars
        ps_s1=[[0]*(size+1) for _ in range(26)]
        ps_s2=[[0]*(size+1) for _ in range(26)]
        for char in range(26):
            for i in range(size):
                ps_s1[char][i+1]=ps_s1[char][i]+int(char==s1[i])
                ps_s2[char][i+1]=ps_s2[char][i]+int(char==s2[i])

        # prefix sum for difference between s1 and s2
        ps_df=[0]*(size+1)
        for i in range(size):
            ps_df[i+1]=ps_df[i]+int(s1[i]!=s2[i])

        def ok(ps_s1,ps_s2,L1,R1,L2,R2):
            if L1>L2: # make sure L1 < L2
                return ok(ps_s2,ps_s1,L2,R2,L1,R1)
            # common case: leftmost and rightmost part should be same
            if get_diff(0,L1-1)>0 or get_diff(max(R1,R2)+1,size-1)>0:
                return False

            # case 1: no union
            # swap 2 parts and the middle part should be same
            # [L1 R1]
            #           [L2 R2]
            if R1<L2:
                return can_swap(L1,R1) and can_swap(L2,R2) and get_diff(R1+1,L2-1)==0

            # case 2: included
            # [L1        R1]
            #    [L2  R2]
            if R2<=R1:
                return can_swap(L1,R1)
            
            # case 3: union
            # [L1   R1]
            #      [L2   R2]
            a=get_ps(ps_s1,L1,R1)
            b=get_ps(ps_s2,L1,L2-1)
            res1=subtract(a,b) # fill left part
            a=get_ps(ps_s2,L2,R2)
            b=get_ps(ps_s1,R1+1,R2)
            res2=subtract(a,b) # fill right part
            return res1!=[] and res2!=[] and res1==res2

        def get_ps(ps,i,j):
            res=[0]*26
            for char in range(26):
                res[char]=ps[char][j+1]-ps[char][i]
            return res

        def get_diff(i,j):
            return ps_df[j+1]-ps_df[i]

        def can_swap(i,j):
            return get_ps(ps_s1,i,j)==get_ps(ps_s2,i,j)

        def subtract(ps1,ps2):
            res=[0]*26
            for char in range(26):
                if ps1[char]<ps2[char]: # not enough
                    return []
                res[char]=ps1[char]-ps2[char]
            return res

        ans=[]
        for a,b,c,d in queries:
            L2=N-1-d # right part reversed
            R2=N-1-c
            ans.append(ok(ps_s1,ps_s2,a,b,L2,R2))

        return ans

mocowcow

題目

解法