LeetCode 2846. Minimum Edge Weight Equilibrium Queries in a Tree

September 4, 2023

周賽361。上週才考過倍增，這週馬上就考進階用法，真變態。
雖說是進階版，但LCA倍增其實算是競賽的常見題目，網路上隨便都找得到模板可以套用。可能因此通過人數比上次還多。

題目

有一個n節點的無向樹，節點編號分別為0到n-1。
輸入二維整數陣列edges，其中edges[i] = [u_i, v_i, w_i]，代表節點u_i和v_i之間存在一條權重為w_i邊。

另外還輸入長度m的二維整數陣列queries，其中queries[i] = [a_i, b_i]。
對於每個查詢queries[i]，要求出使得a_i到b_i路徑上的權重相等所需最少操作次數。
每次操作，你可以將任意邊上的權重改變成任意值。

注意：

每次操作都是獨立的。意味著每次操作前，所有邊的權重都會恢復成初始值
a_i到b_i的路徑是由不同的節點序列所組成，從a_i開始，b_i結束。且序列中相鄰的節點都共享一條邊

回傳長度m的陣列answer，其中answer[i]代表第i次查詢的答案。

解法

雖然說是一棵樹，但沒指定根節點，方便起見都把節點0當作根。

要使得路徑上的權重相等，又要操作次數最小，那就只能把所有權重都改成出現次數最多的那個。
但是怎麼求a和b之間的路徑？先找他們的LCA(最近公共祖先)，從LCA到a的路徑加上LCA到b的路徑，就是完整的路徑。

示意圖

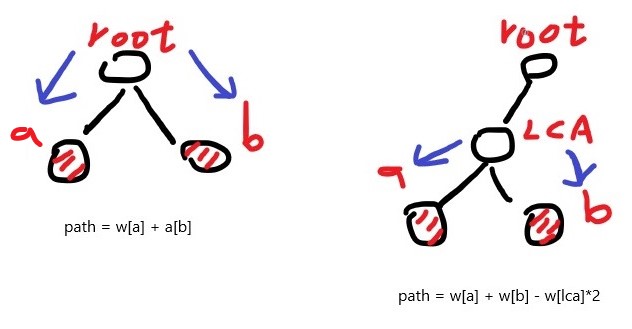
傳統的LCA算法是先使ab深度相等，然後兩者同時向父節點移動，直到ab相等，當前節點就是LCA。
但是本題中節點數量高達10^4，最壞形況下是linked list，每次找LCA都要10^4次移動。查詢也是10^4量級，必須要想辦法優化LCA的算法。

找LCA分成兩個步驟：平衡深度、同時上移。
我們知道a和b深度的差為diff，將diff分解成數個2^j次移動，就是基本款的倍增應用。
但是又怎麼知道要跳多少步才到LCA？這時又要導入二分思想：

跳x步後，a和b相等，代表已經找到LCA或是LCA的祖先。可以保證LCA在當前節點，或是在下方
若a和b不相等，則代表還沒找到LCA。可以保證LCA一定在上方

示意圖

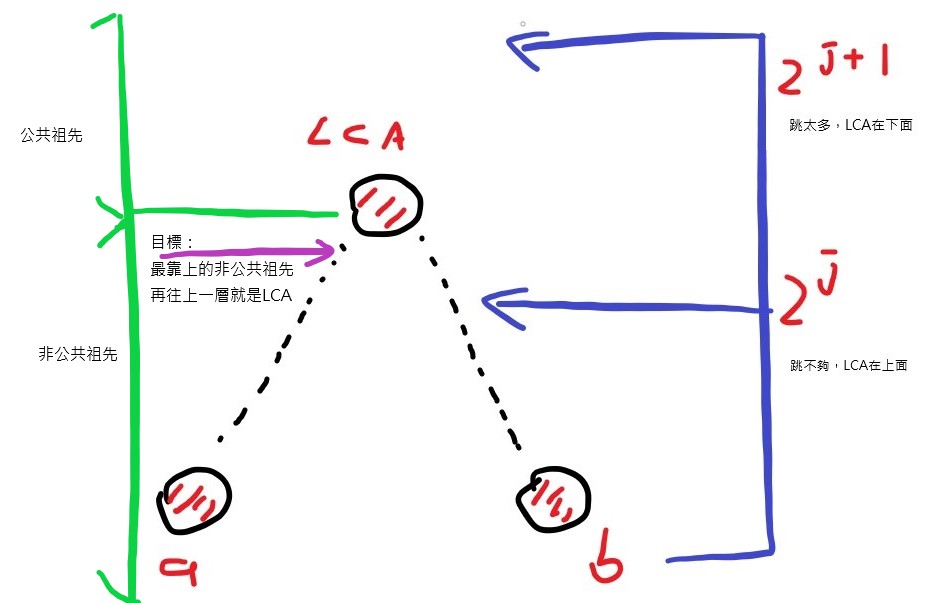
只要找到深度最低，且不是a!=b的位置，再往上一步，就是LCA了。有點類似bisect_right或是upper_bound之後再減1的概念。
接著剛才講的，如果x步會跳到祖先節點，那目標最多只需要x-1步。所以從最大的2^j開始往下檢查，如果跳2^j會相同，就不跳；不會相同就跳。
最後會停在LCA的下方，再往上跳一步就大功告成。

注意：在a或b本身就是LCA的情況下，倍增平衡完深度就可以直接回傳。

最後處理每個查詢[a, b]：

先找到 lca
求 lca 到 a 的路徑和，再上 lca 到 b 的路徑和
找到最高的權重出現次數 max_w，把總邊數 tot 扣掉 max_w 就是答案

預處理倍增O(n log n)，每次查詢O(log n)，整體時間複雜度O( n log n + Q log n )。
空間複雜度O(n log n)。

class Solution:
    def minOperationsQueries(self, n: int, edges: List[List[int]], queries: List[List[int]]) -> List[int]:
        g = [[] for _ in range(n)]
        for a, b, w in edges:
            g[a].append([b, w-1])
            g[b].append([a, w-1])

        ps = [[0]*26 for _ in range(n)]
        parent = [0] * n
        depth = [0] * n

        def dfs(i, fa, dep):
            parent[i] = fa
            depth[i] = dep
            for j, w in g[i]:
                if j == fa:
                    continue
                ps[j] = ps[i].copy()
                ps[j][w] += 1
                dfs(j, i, dep+1)

        dfs(0, -1, 0)

        N = n  # 有多少點
        MX = N.bit_length()  # 最大跳躍次數取 log

        # f[i][jump]: 從 i 跳 2^jump 次的位置
        # -1 代表沒有下一個點
        f = [[-1]*MX for _ in range(N)]

        # 初始化每個位置跳一次
        # 實作細節自行修改
        for i in range(N):
            f[i][0] = parent[i]

        # 倍增遞推
        for jump in range(1, MX):
            for i in range(N):
                temp = f[i][jump-1]
                f[i][jump] = f[temp][jump-1]

        def get_LCA(x, y):
            if depth[x] > depth[y]:
                x, y = y, x

            # 把 y 調整到和 x 相同深度
            diff = depth[y]-depth[x]
            for jump in range(MX):
                if diff & (1 << jump):
                    y = f[y][jump]

            # 已經相同
            if x == y:
                return x

            # 否則找最低的非 LCA
            for jump in reversed(range(MX)):
                if f[x][jump] != f[y][jump]:
                    x = f[x][jump]
                    y = f[y][jump]

            # 再跳一次到 LCA
            return f[x][0]

        def solve(x, y):
            lca = get_LCA(x, y)
            cnt = [0]*26
            for w in range(26):
                cnt[w] = ps[x][w] + ps[y][w] - ps[lca][w]*2
            return sum(cnt)-max(cnt)

        return [solve(*q) for q in queries]

mocowcow

題目

解法