LeetCode 2736. Maximum Sum Queries

June 11, 2023

周賽349。還以為是二分搜，搞了半天sorted list結果TLE。

題目

輸入兩個長度為n的整數陣列nums1和nums2，還有一個二維陣列queries，其中queries[i] = [x_i, y_i]。

對於第i個查詢，要找到最大的nums1[j]+nums2[j]，且滿足nums1[j]>=x_i和nums2[j]>=y_i。若找不到則為-1。

回傳陣列answer，其中answer[i]代表第i個查詢的答案。

解法

nums1對應的是x軸，num2對應y軸。將兩者綁成對，以x軸排序，視作二維座標上的一個紅點；也將queries以x軸排序，視為二維座標上的一個藍點。

以例題1為例：

nums1 = [4,3,1,2], nums2 = [2,4,9,5], queries = [[4,1],[1,3],[2,5]]
排序後
pairs = [[1,9],[2,5],[3,4],[4,2]]
queries = [[1,3],[2,5],[4,1]]

示意圖

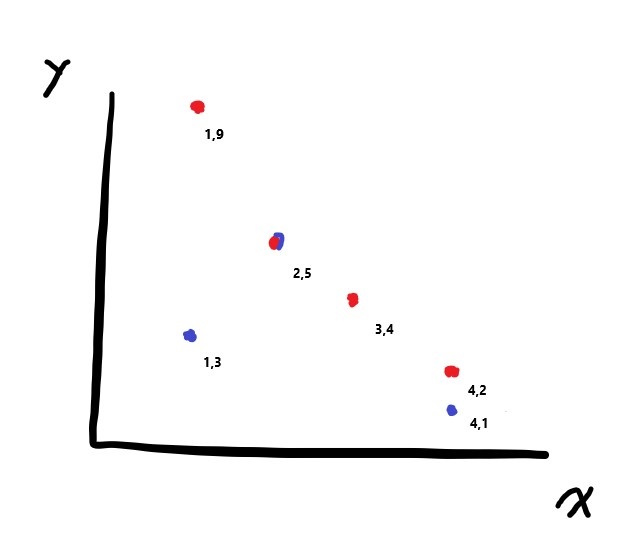
從x軸由大到小處理查詢和數對座標，可以保證先前訪問過的數對x軸一定都大於等於查詢的x軸，這樣只需要維護y軸的區間最大值。
當處理查詢(x,y)時，先把所有x軸也大於等於x的數對加入，然後查詢(x,y)右上方範圍內的最大值。

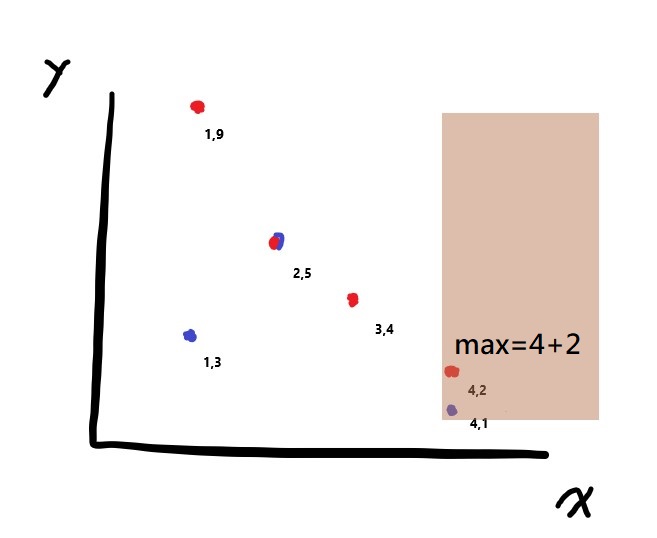
對於查詢(4,1)來說，右上方只有(4,2)這個點，最大值是4+2。
示意圖

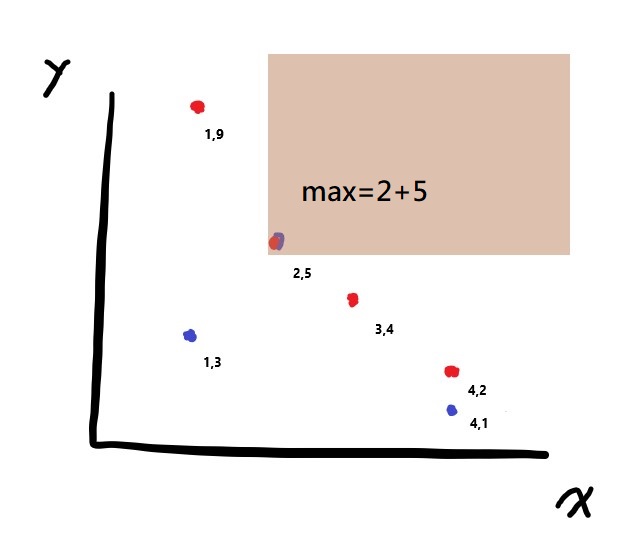
對於查詢(2,5)來說，右上方只有(2,5)這個點，最大值是2+5。
示意圖

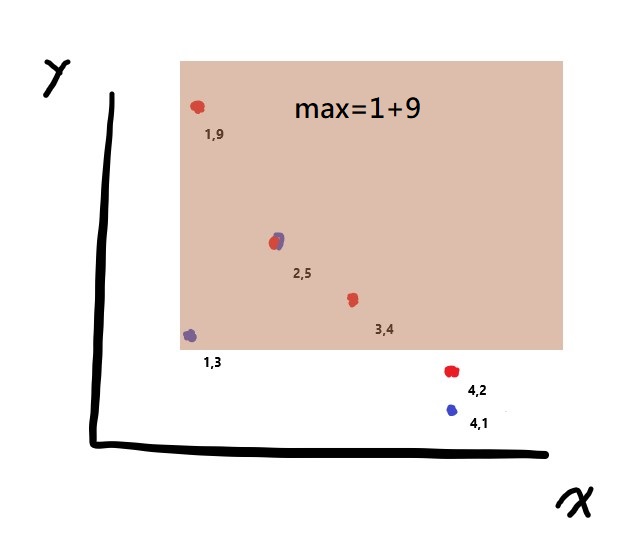
對於查詢(1,3)來說，右上方有(1,9), (2,5)和(3,4)三個點，最大值是1+9。
示意圖

要維護區間的最大值，又是線段樹的主場。
座標上限高達10^9，但是最多只會有10^5個點，可以選擇動態開點或是離散化+普通線段樹。

剛好有做動態開點最大值的模板就直接拿來用了。
需要注意的是：無符合查詢答案是-1，所以初始化最大值應設為-1，而不是0。

時間複雜度O( (N+Q) log MX)，其中N為nums1大小，Q為查詢次數，MX為座標最大值。
空間複雜度O(N log MX)。

class Node:
    __slots__ = ['L', 'R', 'mx', 'left', 'right']

    def __init__(self, L, R, mx):
        self.L = L
        self.R = R
        self.mx = mx
        self.left = self.right = None


class SegmentTree:
    def __init__(self, L, R):
        self.root = Node(L, R, -1)

    def query(self, i, j):
        return self._q(self.root, i, j)

    def _q(self, node, i, j):
        if i > node.R or j < node.L:  # out of range
            return -1
        if i <= node.L and j >= node.R:  # fully covered
            return node.mx
        if not node.left:
            return node.mx
        return max(self._q(node.right, i, j), self._q(node.left, i, j))

    def update(self, i, j, val):
        self._u(self.root, i, j, val)

    def _u(self, node, i, j, val):
        if i > node.R or j < node.L:  # out of range
            return
        if i <= node.L and j >= node.R:  # fully covered
            node.mx = val
            node.left = node.right = None
            return
        M = (node.L+node.R)//2
        if not node.left:
            node.left = Node(node.L, M, node.mx)
            node.right = Node(M+1, node.R, node.mx)
        if M >= i:
            self._u(node.left, i, j, val)
        if M < j:
            self._u(node.right, i, j, val)
        node.mx = max(node.left.mx, node.right.mx)


class Solution:
    def maximumSumQueries(self, nums1: List[int], nums2: List[int], queries: List[List[int]]) -> List[int]:
        MX=10**9
        N=len(nums1)
        Q=len(queries)
        pairs=sorted((a,b,a+b) for a,b in zip(nums1,nums2))
        qs=sorted((x,i) for i,x in enumerate(queries))
        tree=SegmentTree(1,MX)
        ans=[0]*Q
        pid=N-1
        
        for (x,y),qid in reversed(qs):
            while pid>=0 and pairs[pid][0]>=x:
                a,b,ab=pairs[pid]
                if tree.query(b,b)<ab:
                    tree.update(b,b,ab)
                pid-=1
            ans[qid]=tree.query(y,MX)
        
        return ans

假設右方有個座標(x,y)，而左方正在處理(a,b)，由於是從大到小處理x軸，所以a一定小於等於x。

如果b < y，保證x+y > a+b，所以(a,b)這點就永遠不會是查詢的目標
如果b = y，因為x > a，同樣的(a,b)也不需要考慮
如果b > y，就可以看看要不要留

這時新加入的(a,b)，如果值比右方某些的座標值更大，那麼就可以丟掉右方的座標了。例如：

左方座標(10,1000)，右方座標(20,20)
之後處理到的查詢x軸肯定都小於等於10
不管如何，選擇(10,1000)肯定比(20,20)更好，所以丟掉(20,20)

丟掉完不要的(x,y)之後，記得把新的(a,b)加入堆疊。
基於丟掉較小的x+y值，從堆疊底往上看，x+y會呈現單調遞減。
又因為a <= x和a+b > x+y，保證b大於y，從堆疊底往上看，y會呈現單調遞增。

之後每次查詢只考慮y軸，y軸越低越可能獲得更大的x+y；反之，y軸越高能獲得的x+y值越小。
這時透過二分搜在堆疊上找到第一個大於等於查詢y的座標點，正是x+y值最大的地方。

維護單調堆疊只需要O(N)，但是每次查詢還是要O(log N)。整體時間複雜度O(N + Q log N)，其中N為nums1大小，Q為查詢次數。
空間複雜度O(N)。

class Solution:
    def maximumSumQueries(self, nums1: List[int], nums2: List[int], queries: List[List[int]]) -> List[int]:
        N=len(nums1)
        Q=len(queries)
        pairs=sorted((a,b,a+b) for a,b in zip(nums1,nums2))
        qs=sorted((x,i) for i,x in enumerate(queries))
        st=[]
        ans=[-1]*Q
        pid=N-1
        
        for (x,y),qid in reversed(qs):
            while pid>=0 and pairs[pid][0]>=x:
                a,b,ab=pairs[pid]
                pid-=1
                if st and st[-1][0]>=b: # (a,b)在(x,y)左下，不考慮
                    continue
                while st and st[-1][1]<=ab: # 若(a+b)>=(x+y)，因a<=x所以保證b>=y，之後不再考慮(x,y)
                    st.pop()
                st.append([b,ab])

            j=bisect_left(st,[y,0])
            if j<len(st):
                ans[qid]=st[j][1]
        
        return ans

mocowcow

題目

解法