LeetCode 2719. Count of Integers
周賽348。又忘記取模吃一次WA,好慘。
題目
輸入兩個數字字串num1和num2,以及兩個整數max_sum和min_sum。
一個好的整數x必須滿足:
- num1 <= x <= num2
- min_sum <= digit_sum(x) <= max_sum
求有多少好的整數。答案很大,先模10^9+7後回傳。
注意:digit_sum(x)指的是x中所有數字的加總。
解法
這種求範圍內多少數符合特別條件的,基本上就是數位DP。
要找符合[num1, num2]區間的x很麻煩,可以轉換成[0, nums2]中 扣掉 [0, nums1 - 1]中的個數。
同理,位數總和digit_sum也要介於[max_sum, min_sum]之間,轉換成[0, max_sum]中 扣掉 [0, min_sum - 1]中的個數。
定義為f(s, mx_digit)為:小於等於s,且位數和小於等於mx_digit的好的整數個數。
題目要求的是數字s介於[num1, num2]之間,且位數和介於[max_sum, min_sum]之間。
根據排容原理,公式為:
f(num2, max_sum) - f(num1 - 1 , max_sum) - f(num2 , min_sum - 1) + f(num1 - 1 , min_sum - 1)
做4次數位dp就可以求出,也就是附圖中的紅色區塊。
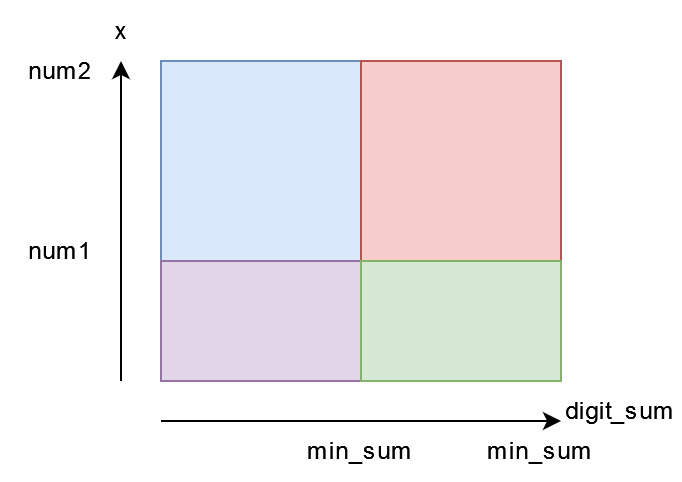
最後剩下數位dp的實作。
定義dp(i,cnt_digit,is_limit,is_num):當位數和為cnt_digit時,從i~N-1的部分共有多少種有效的選法。
is_limit當前數字是否受限於最大值s的第i位數,這會根據高位數的選項而改變;is_num則代表高位所選過的數字是否為有效的數字。
轉移方程式:只有當is_limit為true,且選擇同時當前最高位的數字,才需要從is_limit=true的狀態轉移過來,嚴格來說整個過程中總共只有N個狀態。
如果is_limit為true,則只能選擇0~s[i]的數字,才不會超過規定的數字上限;否則0~9可以任選。
base case:當cnt_digit超過規定的位數和mx_digit,之後不管怎樣選都不合法,直接回傳0。
當i等於N,代表所有位數都選完,而且不超過mx_digit,這時is_num=true代表所選的值不全為0,是一個有效值,可以和空字串組成一種可能;否則值為0,不在題目要求的有效範圍內,回傳0。
dp共有四個狀態:i的狀態有N種;cnt_digit的狀態為mx_digit種,也可能受限於9N種;is_limit和is_nums都只有2種。
每個狀態最多轉移10次,然後要4次dp,為O(4 * 10 * N * M * 2 * 2),其中N為s大小,M為min(9N,max_sum)。
去掉常數後,整體時間複雜度O(N*M)。
空間複雜度O(N*M)。
class Solution:
def count(self, num1: str, num2: str, min_sum: int, max_sum: int) -> int:
MOD=10**9+7
def f(s,mx_digit):
N=len(s)
@cache
def dp(i,cnt_digit,is_limit,is_num):
if cnt_digit>mx_digit:
return 0
if i==N:
return is_num
up=int(s[i]) if is_limit else 9
down=0 if is_num else 1
ans=0
if not is_num:
ans=dp(i+1,0,False,False)
for j in range(down,up+1):
new_limit=is_limit and j==up
ans+=dp(i+1,cnt_digit+j,new_limit,True)
return ans%MOD
return dp(0,0,True,False)
num1=str(int(num1)-1)
min_sum-=1
ans=f(num2,max_sum)-f(num1,max_sum)-f(num2,min_sum)+f(num1,min_sum)
return ans%MOD
仔細想想,is_num這個狀態根本不需要,因為:
- min_sum至少會是1,但是全部選0的位數和是0,根本不會被算進去
- 就算會被算進去,在排容的時後也會被消掉,不影響答案
而且也不需要切成四塊,既然我們都可以在dp裡面判斷是否超過max_sum,那麼在base case的時候判斷是否至少min_sum就可以。
f只需要字串s一個參數,答案簡化成f(num2)-f(num1 - 1)。
class Solution:
def count(self, num1: str, num2: str, min_sum: int, max_sum: int) -> int:
MOD=10**9+7
def f(s):
N=len(s)
@cache
def dp(i,cnt_digit,is_limit):
if cnt_digit>max_sum:
return 0
if i==N:
return cnt_digit>=min_sum
up=int(s[i]) if is_limit else 9
ans=0
for j in range(up+1):
new_limit=is_limit and j==up
ans+=dp(i+1,cnt_digit+j,new_limit)
return ans%MOD
return dp(0,0,True)
num1=str(int(num1)-1)
ans=f(num2)-f(num1)
return ans%MOD
如果在別的語言,num1的值可能高達10^22,超過long的上限,沒辦法轉成數字-1後轉回字串。
這時只能用f(num2)-f(num1),並且單獨判斷num1,若位數和介於min_sum和max_sum間,則將答案補回1。
另外一個問題是手刻記憶化搜索,到底要記憶哪些狀態?
剛才提到過is_limit=true的狀態最多只有N個,而且也只會被用到一次,那其實不必記憶他。
例如:
num = “123”
i = 0時,選1才符合is_limit
i = 1時,選12才符合is_limit
i = 2時,選123才符合is_limit
省略掉is_limit這個維度,只有在is_limit=false才做記憶化。
var MOD int=1e9+7
func count(num1 string, num2 string, min_sum int, max_sum int) int {
var f func(s string) int
f=func (s string) int{
memo:=make([][]int,30)
for i:=range memo{
memo[i]=make([]int,405)
for j:=range memo[i]{
memo[i][j]=-1
}
}
var dp func(i, cnt_digit int, is_limit bool) int
dp=func(i, cnt_digit int, is_limit bool) int{
if cnt_digit>max_sum{
return 0
}
if i==len(s){
if cnt_digit>=min_sum{
return 1
}
return 0
}
if !is_limit && memo[i][cnt_digit]!=-1{
return memo[i][cnt_digit]
}
res:=0
up:=9
if is_limit{
up=int(s[i]-'0')
}
for j:=0;j<=up;j++{
new_limit:=is_limit && j==up
res+=dp(i+1,cnt_digit+j,new_limit)
}
res=(res+MOD)%MOD
if !is_limit{
memo[i][cnt_digit]=res
}
return res
}
return dp(0,0,true)
}
ans:=f(num2)-f(num1)
cnt:=0
for _,c:=range num1{
cnt+=int(c-'0')
}
if min_sum<=cnt && cnt<=max_sum{
ans+=1
}
return (ans+MOD)%MOD
}