LeetCode 2699. Modify Graph Edge Weights

May 23, 2023

周賽346。最近Q4圖論出現次數有夠多，但這題難度也太誇張，不到一百人做出來。

題目

有一個n節點的無向有權連通圖，節點編號由0~n-1。
輸入二維整數陣列edges，其中edges[i] = [a_i, b_i, w_i]，代表a_i和b_i之間存在一條邊權為w_i的邊。

有部分的邊權為-1，而其他都是正數。

你的目標是將所有邊權為-1的邊修改成介於[1, 2^10+9]內的正整數，並使得從節點source到節點destination之間的最短距離等於target。若有多種修改方案，可選擇任一種。

若存在合法方案，則依任意順序回傳包含所有邊的陣列(包含沒修改過的)。若不存在，則回傳空陣列。

注意：你不可以修改初始邊權為正數的邊。

解法

有兩個比較容易發現的特殊形況：

將特殊邊最小化成1，最短路超過target，不可能再將最短路縮短
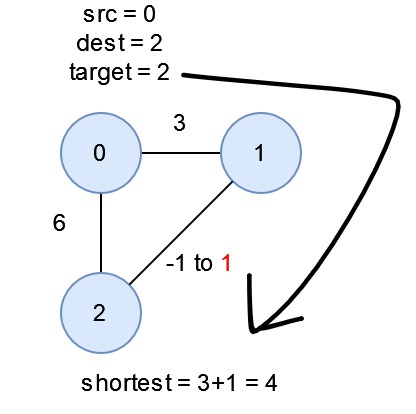
將特殊邊最大化成2e9，最短路不足target，不可能再將最短路增加

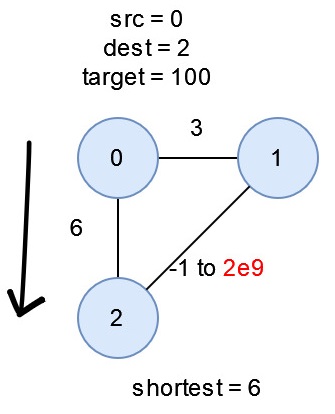
先跑一次dijkstra，把所有特殊邊都設成1，若超過target則直接回傳空陣列。
然後跑第二次dijkstra，根據第一次所算出的各點最短路徑dis1，來計算出可以把特殊邊改多大的值。
如果改完還是不足target，一樣回傳空陣列；否則將沒用到的特殊邊改成任意值，回傳edges。

回顧一下dijkstra的核心思想：不斷選擇最短的路徑，並繼續從該點移動，直到走到終點為止。
當選擇最短的路徑，並處於X點時，和X相鄰的所有點Y都可能是下一個最短路的候補。而Y走到終點dest距離已經在第一次的dijkstra中算出。
假設結構為[src -> X -> Y -> dest]。為了通過修改X到Y的路徑而使最短路等於target，得到以下等式：

target = [src -> X] + [X -> Y] + [Y -> dest]
[src -> X]是第二次dijkstra從起點走到X也距離，也就是當前的dis[X]
[X -> Y]是要修改的距離，記為w
[Y -> dest]是第一次dijkstra中，Y走到終點的最短路。可以透過dis1[dest]-dis[y]求出
得到target = dis[X] + w + (dis1[dest] - dis1[Y])
移項得w = target - dis[X] - dis1[dest] + dis1[Y]

但要特別注意，修改後的邊權只能介於[1, 2e9]之間，如果公式求出的w小於1，則為非法答案，只能沿用最小值1。
那w會不會超過2e9？答案是不會，如果單個邊需要超過2e9，那麼在第一次dijkstra時就被過濾掉了。

時間複雜度O(n + M log M)，其中M為edges大小。
空間複雜度O(n + M)。

class Solution:
    def modifiedGraphEdges(self, n: int, edges: List[List[int]], source: int, destination: int, target: int) -> List[List[int]]:
        g=[[] for _ in range(n)]
        for id,(a,b,_) in enumerate(edges):
            g[a].append([b,id])
            g[b].append([a,id])
        
        def dijkstra_first():
            dis=[inf]*n
            h=[[0,source]]
            while h:
                cost,i=heappop(h)
                if cost>dis[i]:
                    continue
                dis[i]=cost
                if i==destination:
                    break
                for j,id in g[i]:
                    w=edges[id][2]
                    if w==-1: # 特殊邊設成1
                        w=1
                    new_cost=cost+w
                    if new_cost<dis[j]:
                        dis[j]=new_cost
                        heappush(h,[new_cost,j])
            return dis
        
        def dijkstra_second():
            dis=[inf]*n
            h=[[0,source]]
            while h:
                cost,i=heappop(h)
                if cost>dis[i]:
                    continue
                dis[i]=cost
                if i==destination:
                    break
                for j,id in g[i]:
                    w=edges[id][2]
                    if w==-1: # 調整特殊邊
                        w=1
                        new_w=target-dis[i]-dis1[destination]+dis1[j]
                        if new_w>1: # 特殊邊最小為1，只能放大
                            w=new_w
                            edges[id][2]=new_w
                    new_cost=cost+w
                    if new_cost<dis[j]:
                        dis[j]=new_cost
                        heappush(h,[new_cost,j])
            return dis
        
        # 把所有特殊邊設成最小值
        # 如果最短路還大於target
        # 代表不可能有答案
        dis1=dijkstra_first()
        if dis1[destination]>target:
            return []
        
        # 把所有特殊邊設成可能最大值
        # 如果最短路還是不足target
        # 也不可能有答案
        dis2=dijkstra_second()
        if dis2[destination]<target:
            return []
        
        # 把沒用到的特殊邊都隨便填上
        for e in edges:
            if e[2]==-1:
                e[2]=1
                
        return edges

mocowcow

題目

解法