LeetCode 2673. Make Costs of Paths Equal in a Binary Tree

May 7, 2023

周賽344。老實說我覺得這輸入有點整人，說節點從1開始算，但是對應的值卻是0開始算，兩者統一不是更好。

題目

輸入整數n，代表一顆有n個節點的prefect binary tree，節點編號分別為1~n。
根節點編號為1，對於每個節點i，左子節點的編號為2*1，右子節點編號為i*2+1。

每個節點都有一個成本，由整數長度n的陣列cost表示。其中cost[i]代表節點編號i+1的成本。
你可以將任意節點的成本增加1任意次。

求使得從根節點到所有葉節點的路徑成本相同，最少需要增加成本幾次。

解法

一開始想錯方向，以為把每層的節點都改到跟最大的一樣就行，但碰到以下例子就會發現完全不對：
示意圖
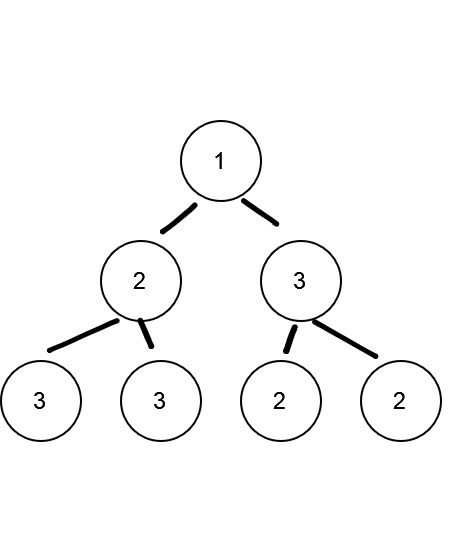
每條路徑都是[1,3,2]或[1,2,3]，根本不用改就相同。

後來想想，正確應是使每條路徑等於成本最大的路徑。
如果我們從上往下找，並不知道子節點會出現什麼值，更不用說判斷成本相不相同。所以先dfs遍歷一次，找出最大的路徑。
示意圖
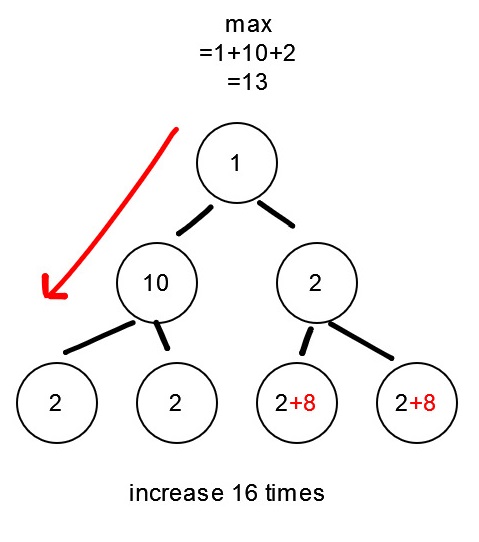
如圖，最大的路徑應為13，必須將其他路徑修改數次，使之變成13。
但如果兩條路徑擁有共通的父節點，那麼在父節點上修改，只需要一半的修改次數。

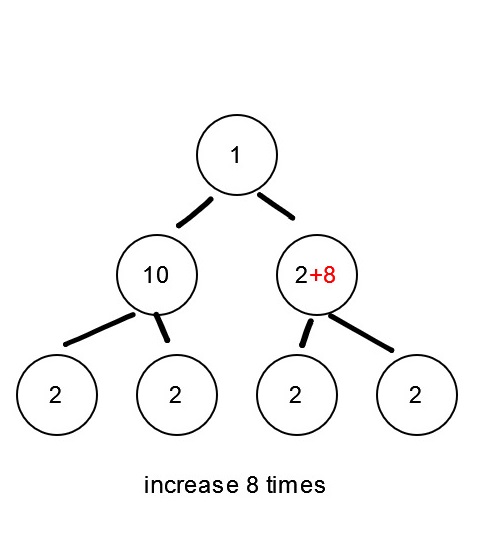
因此維護陣列inc，透過後序dfs求出各節點所需的修改次數inc[i]。
若當前節點i為葉節點，則修改次數inc[i]為mx-sm；否則為左右節點提出的共通值mn，並將左右扣掉mn。

最後回傳inc的加總就是答案。
順帶一提，根節點inc[1]永遠會是0。若不為0的狀況下，代表左右節點有共通的提取值，代表有冗於的修改次數，必定不是最佳答案。

時間複雜度O(n)。
空間複雜度O(n)。

class Solution:
    def minIncrements(self, n: int, cost: List[int]) -> int:
        cost=[0]+cost
        inc=[0]*(n+1)
        mx=0
        
        def dfs(i,sm):
            nonlocal mx
            l=i*2
            r=i*2+1
            sm+=cost[i]
            if l<=n:
                dfs(l,sm)
                dfs(r,sm)
            else: # leaf
                mx=max(mx,sm)
                
        dfs(1,0)
        
        def dfs2(i,sm):
            l=i*2
            r=i*2+1
            sm+=cost[i]
            if l<=n:
                dfs2(l,sm)
                dfs2(r,sm)
                mn=min(inc[l],inc[r])
                inc[i]=mn
                inc[l]-=mn
                inc[r]-=mn
            else: # leaf
                inc[i]=mx-sm
        
        dfs2(1,0)
        
        return sum(inc)

dfs改成迴圈，並直接在cost上操作。
將父節點的的成本加到子節點上，葉節點就會是路徑的總和。
在從最後一個節點向前遍歷，若是葉節點則求出修改次數；否則從子節點提取出共通值mn，並從子節點扣除mn。

時間複雜度O(n)。
空間複雜度O(n)。

class Solution:
    def minIncrements(self, n: int, cost: List[int]) -> int:
        cost=[0]+cost
        
        for i in range(1,n+1):
            l=i*2
            r=i*2+1
            if l<=n:
                cost[l]+=cost[i]
                cost[r]+=cost[i]
                
        mx=max(cost)
        for i in range(n,-1,-1):
            l=i*2
            r=i*2+1
            if l<=n:
                mn=min(cost[l],cost[r])
                cost[i]=mn
                cost[l]-=mn
                cost[r]-=mn
            else:
                cost[i]=mx-cost[i]

        return sum(cost)

上面兩種方法都是站在子節點的視角來考慮要修改幾次。那如果是站在父節點的視角呢？
對於某節點i所產生的兩個路徑l和r，從根到i為止的成本都是共通的，所以只要將l和r的成本調整相同。
而l和r所產生的路徑也是同理，變成一個遞迴的子問題。最後會從最下層的非葉節點開始向上處理。

示意圖

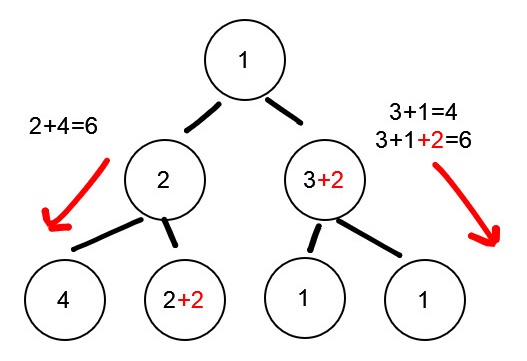
如圖，對於根節點來說，左節點出發的所有路徑都成本都為6，而右節點3路徑都為4。這時應該在節點3再修改2次，使兩邊平衡。答案應為4次修改。

因此，我們只需要一次後序dfs，先算出子節點的修改次數，並加入答案後，回傳修改後子節點的成本供父節點使用。

時間複雜度O(n)。
遞迴最多log n層，空間複雜度O(log n)。

class Solution:
    def minIncrements(self, n: int, cost: List[int]) -> int:
        ans=0
        cost=[0]+cost
        
        def dfs(i):
            nonlocal ans 
            if i>n:
                return 0
            l=dfs(i*2)
            r=dfs(i*2+1)
            ans+=abs(l-r)
            return max(l,r)+cost[i]
        
        dfs(1)
        
        return ans

一樣也可以改成迴圈。
根據complete binary tree特性，編號第1~(n/2)都是非葉節點，而(n/2)+1~n的都是葉節點，直接從n/2開始像前遍歷即可。

時間複雜度O(n)。
不需要遞迴，空間複雜度O(1)。

class Solution:
    def minIncrements(self, n: int, cost: List[int]) -> int:
        ans=0
        cost=[0]+cost
        
        for i in range(n//2,0,-1):
            l=cost[i*2]
            r=cost[i*2+1]
            ans+=abs(l-r)
            cost[i]+=max(l,r)
        
        return ans

mocowcow

題目

解法