LeetCode 2615. Sum of Distances

April 11, 2023

周賽339。跟前幾次周賽Q3很像，這題放到Q2好像不太友善。

題目

輸入整數陣列nums。
存在一個相同長度的陣列arr，其中arr[i]等於所有|i-j|的總和，其中nums[j]==nums[i]，且j!=i。如果不存在任何j，則將arr[i]設為0。

回傳陣列arr。

解法

相似題2602. minimum operations to make all array elements equal。

只有nums[i]值相同的索引才會互相影響，所以先依照nums[i]的值將索引分組。

先從最簡單的例子來看：

nums = [1,1,1]
對於nums[0]來說，左方(含自己)的索引有[0]，右方索引有[1,2]
而左方的索引都小於等於i，所以要拿i去扣除；右方索引都大於i，用索引總和扣掉i
所以arr[0] = 左方(0-0) + 右方(1-0) + (2-0) = 3
對於nums[1]來說，左方(含自己)的索引有[0,1]，右方索引有[2]
所以arr[1] = 左方(1-0) + (1-1) + 右方(3-1) = 4
對於nums[2]來說，左方(含自己)的索引有[0,1,2]，右方索引有[]
所以arr[2] = 左方(2-0) + (2-1) + (2-2) = 3

對於索引i來說：

總共有M個索引和nums[i]相同
從0到i為止共有(i+1)個索引，這些索引都小於等於i，所以用i*(i+1)扣掉這些索引的總和。
而右方共有(M-i-1)個索引大於i，所以用這些索引的總和扣掉(M-i-1)*(i+1)

示意圖

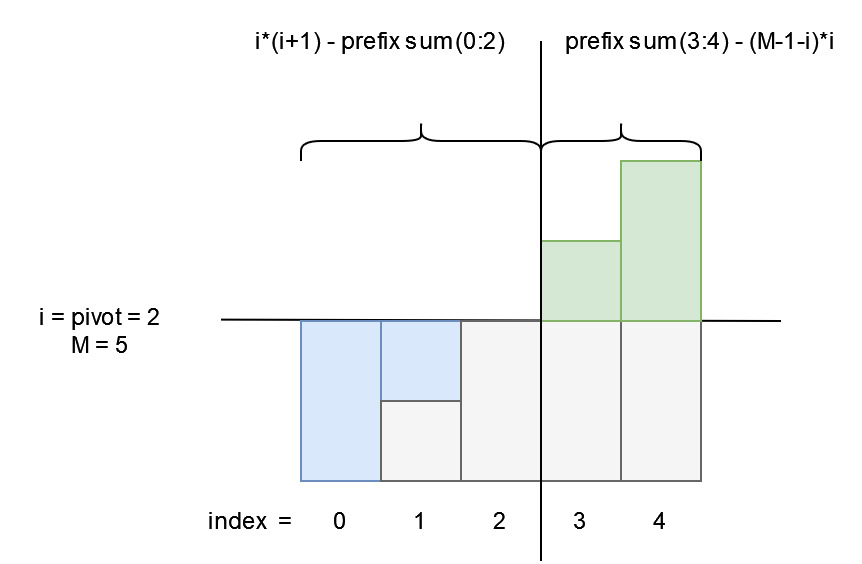
我們可以透過二分搜找到每個索引在組內的相對位置，每次O(log M)。
索引加總都是連續的區塊，所以可以預處理前綴和，之後每次查詢區間和都是O(1)。

最差情況下N個元素都相同，使得二分搜複雜度為O(log N)，整體時間複雜度O(N log N)。空間複雜度O(N)。

class Solution:
    def distance(self, nums: List[int]) -> List[int]:
        N=len(nums)
        d=defaultdict(list)
        ans=[0]*N
        
        # group indexes by nums[i]
        for i,n in enumerate(nums):
            d[n].append(i)
            
        # build prefix sum for each group
        ps_group={}
        for k,vals in d.items():
            ps_group[k]=list(accumulate(vals,initial=0))
                
        for i,n in enumerate(nums):
            pivot=bisect_left(d[n],i)
            ps=ps_group[n]
            # 0 ~ pivot
            # total (pivot+1) elements
            left=i*(pivot+1)-(ps[pivot+1])
            # pivot+1 ~ N-1
            # total (N-1-pivot) elements
            right=(ps[-1]-ps[pivot+1])-i*(len(d[n])-1-pivot)
            ans[i]=left+right
        
        return ans

參考大神的解答，發現有很重要的優化：因為分組時是按照順序加入索引，所以遍歷每一組的時候索引依然保持有序，因此不需要二分就可以知道當前索引i是該組別中的第pivot個元素。

而在遍歷組別中所有元素的同時，也能得知原本的索引，因此可以直接寫入答案。

時間複雜度O(N)。空間複雜度O(N)。

class Solution:
    def distance(self, nums: List[int]) -> List[int]:
        N=len(nums)
        d=defaultdict(list)
        ans=[0]*N
        
        for i,n in enumerate(nums):
            d[n].append(i)
            
        for k,v in d.items():
            ps=list(accumulate(v,initial=0))
            # there are M elements in the group
            # left part = (pivot+1)
            # right part = (M-1-pivot)
            for pivot,i in enumerate(d[k]):
                left=i*(pivot+1)-ps[pivot+1]
                right=ps[-1]-ps[pivot+1]-(i*(len(d[k])-1-pivot))
                ans[i]=left+right
        
        return ans

另外一種思路是：當pivot向右移動時，差值為diff。左邊的所有數都會增加diff，而右邊的都會減少diff。
例如：

idx = [3,4,5]
pivot = 0時，總和為(3-3) + (4-3) + (5-3) = 3
pivot移動到1，diff = (4-3)，有1個元素增加了diff、2個數字減少了diff
pivot = 1時，總和為3 + 1*diff -2*diff = 2
pivot移動到2，diff = (5-4)，有2個元素字增加了diff、1個數字減少了diff
pivot = 2時，總和為2 + 2*diff -1*diff = 3

可以看出，若從j-1移動到j，會有j個元素減少diff，然後M-j個元素增加diff。

時間複雜度O(N)。空間複雜度O(N)。

class Solution:
    def distance(self, nums: List[int]) -> List[int]:
        N=len(nums)
        d=defaultdict(list)
        ans=[0]*N
        
        for i,n in enumerate(nums):
            d[n].append(i)
            
        for v in d.values():
            M=len(v)
            tot=sum(x-v[0] for x in v)
            ans[v[0]]=tot
            for i in range(1,M):
                diff=v[i]-v[i-1]
                inc=diff*i
                dec=diff*(M-i)
                tot+=inc-dec
                ans[v[i]]=tot
        
        return ans

mocowcow

題目

解法