LeetCode 2612. Minimum Reverse Operations

April 7, 2023

周賽339。搞了好幾天才完全弄懂，不愧是小於100人通過的難題，細節有夠多。

題目

輸入整數n和p，其中p介於[0, n-1]之間。代表有一個長度為n的陣列arr，起初除了索引p是1以外，其他索引都是0。

另外還有整數陣列banned，其中包含了一些索引，代表arr[banned[i]]必須永遠為0。保證p不在banned之中。

你可以對arr進行任意次操作。每次操作，你可以選擇一個長度為k的子陣列，將其整個翻轉。但是翻轉後的1不可以跑到banned中的任何索引上。也就是說每次操作完，arr[banned[i]]還是0。

回傳長度為n的陣列ans，其中ans[i]代表使1跑到arr[i]的最小操作次數。若不可能則記為-1。

解法d

有個大前提：翻轉的子陣列必須包含1，否則1不會移動位置。

假設1在索引i，要翻轉的子陣列大小為k，範圍為[lb:rb]：

若要使i翻轉後盡可能的靠左，那i必須在子陣列的最右端。而子陣列右邊界rb為i，左邊界lb則為i-k+1
若要盡可能靠右，那i必須要在子陣列最左端。而子陣列左邊界lb為i，右邊界rb則為i+k-1

但是如果因為k太大，如果把i放在左右端點上會導致子陣列超出邊界，例如：

i = 1, k = 3
rb = 1, lb = i - k + 1
lb = 1 - 3 + 1 = -1
-1為非法索引

這時只能將左邊界lb設為0，右邊界rb為k-1。索引i位於[lb:rb]之中，根據對稱性，翻轉後i的位置為lb+rb-i = (0)+(k-1)-i = k-1-i。
同理，i太過靠右時，右邊界rb只能設為k-1。翻轉後i的位置為lb+rb-i = (n-1-k+1)+(n-1)-i = 2n-1-k-i。

示意圖

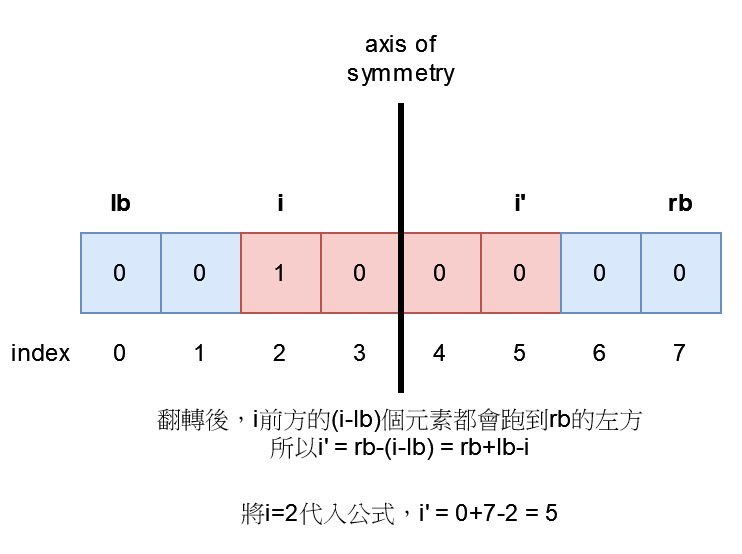
所以i翻轉後的可能位置記為[L:R]，其中L為max(i-k+1, k-1-i)，而R為min(i-k+1, 2n-1-k-i)。

然後來看看各種大小子陣列翻轉的情形。不考慮出界，設i=3。先看看k=2時：

子陣列[2:3]，翻轉後i=2
子陣列[3:4]，翻轉後i=4

再來看看k=3：

子陣列[1:3]，翻轉後i=1
子陣列[2:4]，翻轉後i=3
子陣列[3:5]，翻轉後i=5

示意圖

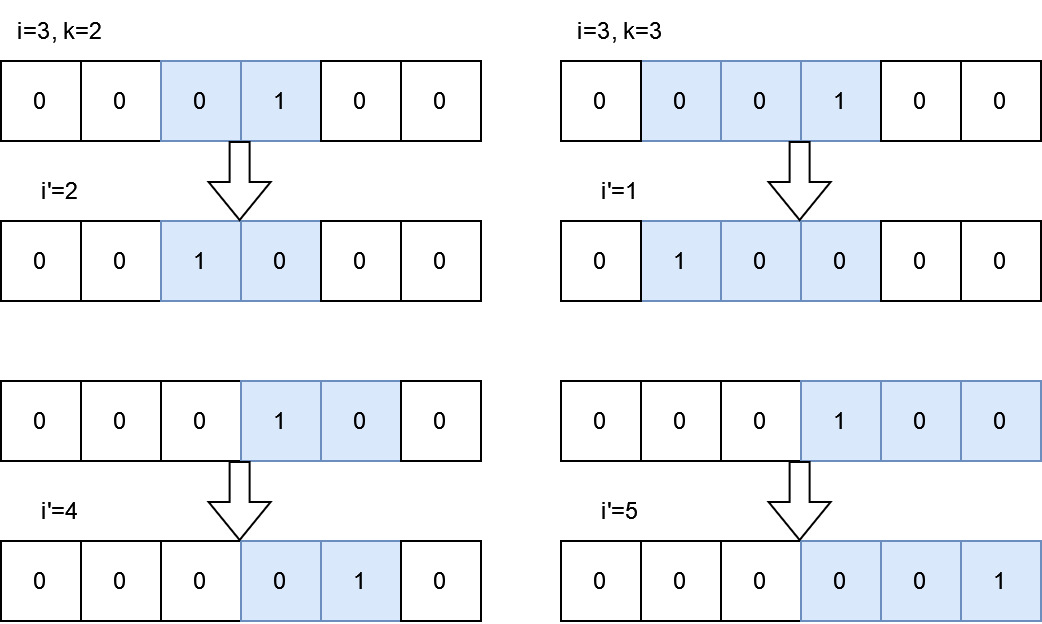
會發現大小為k的子陣列，候選索引差值為2的倍數，奇偶性保持一致。換句話說，如果翻轉後的可能區間為[L:R]，則可能的索引為[L, L+2, … R-2, R]。
而當k為偶數，i翻轉後位置的奇偶性會改變；k為奇數時，則不改變。

而題目要求的是最少翻轉次數，很明顯是bfs。但每次窮舉[L:R]的話同個索引會被訪問到很多次，時間複雜度為O(Nk)，肯定超時。
因為[L:R]是一個連續的區間，所以可以用sorted list來維護尚未訪問過的索引。先以二分搜找到第一個大於等於L的元素，之後不斷刪除，直到當前元素超過R為止。
又因為每個候選索引的差為2，可以把sorted list分成兩個，分別處理奇數偶數的情形。

根據之前提到的：k為偶數時會改變i的奇偶性，要使i加1才能對應到正確的候選索引。
更聰明的方法是直接看L的奇偶，反正不會錯。

最後不要忘記banned裡面的索引不能走，初始化的時候不要加入任何在banned中的索引。

每次二分為O(log n)，但每個索引最多被刪除一次，整體時間複雜度O(n log n)。空間複雜度O(n)。

from sortedcontainers import SortedList

class Solution:
    def minReverseOperations(self, n: int, p: int, banned: List[int], k: int) -> List[int]:
        ban=set(banned)
        idx=[SortedList() for _ in range(2)] # seperate indexes by parity
        ans=[-1]*n
        
        for i in range(n):
            if i not in ban and i!=p:
                idx[i%2].add(i)
                
        step=0
        q=deque()
        q.append(p)
            
        while q:
            for _ in range(len(q)):
                i=q.popleft()
                ans[i]=step
                rmv=[]
                L=max(i-k+1,k-1-i) # leftmost idx
                R=min(i+k-1,2*n-i-k-1) # rightmost idx
                # parity=i+int(k%2==0)
                parity=L
                sl=idx[parity%2]
                j=sl.bisect_left(L)
                
                while j<len(sl) and sl[j]<=R:
                    rmv.append(sl[j])
                    j+=1
                    
                for x in rmv:
                    q.append(x)
                    sl.remove(x)
                
            step+=1
                
        return ans

mocowcow

題目

解法d