LeetCode 2608. Shortest Cycle in a Graph

雙周賽101。我一直卡在不知道如何處理奇數環和偶數環。正確應該在入佇列之前就判斷環，而不是進去後才判斷，有夠尷尬。
最近官方水準越來越垃圾，不抓作弊就算了，還直接這種google名稱就可以找到答案的題目，直接冒出兩三千個作弊哥貼答案，誠實的同學們真的被打個半死。

題目

有個n節點的雙向圖，節點編號分別為0~n-1。
二維陣列edges代表圖中的邊，其中edges[i] = [u_i, v_i]代表頂點u_i和v_i之間存在一條邊。
兩節點之間最多只會有一條邊，且節點不會有邊連到自己。

求圖中最短的環長度。如果沒有環則回傳-1。

解法

若一個圖中存在多個環，使用dfs沒辦法保證一定走到最短的路徑，故無法找到最小環。
使用bfs的話，從某個節點出發，只要某個節點被訪問第二次，必定是由兩條不同的路徑抵達，而這兩條路徑連接起來正好是一個環。

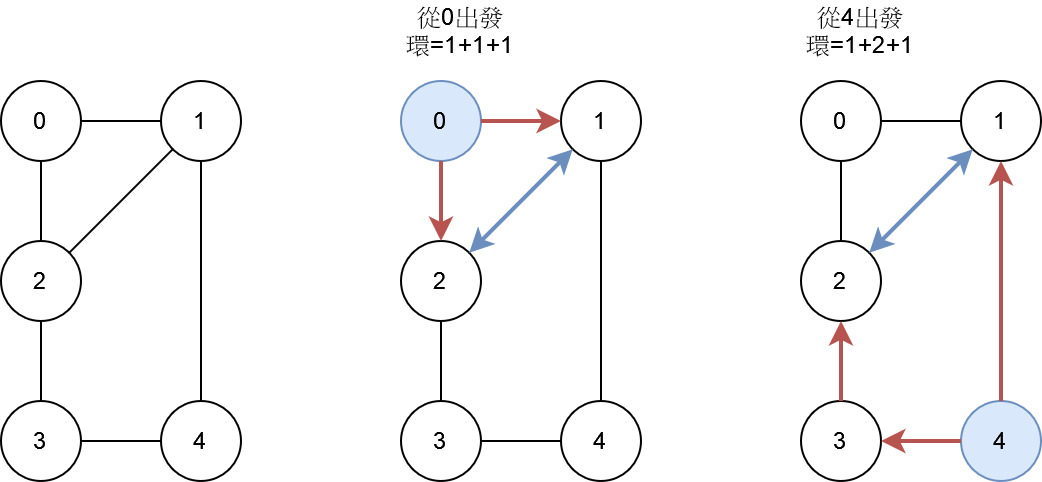
但根據出發點的不同，最先找到的環也不同。所以必須窮舉每個節點做為出發點各bfs一次，看哪個環最小。
而且第一個找到的環也不一定是最小環，所以還是要跑完整個bfs流程，千萬不可以提早退出。

在bfs時還有另一個問題：要如何判斷一個點是自己剛走過的，還是別條路徑走過的？
只要在佇列中額外維護一個父節點變數fa，窮舉相鄰節點j時，若j=fa則略過不處理。若不為父節點且已經被訪問過，則代表找到環，以兩條路徑的長度加上1即為環長。

時間複雜度O(NM)。空間複雜度O(N+M)。

class Solution:
    def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:
        g=defaultdict(list)
        for a,b in edges:
            g[a].append(b)
            g[b].append(a)
        
        def bfs(src):
            cycle=inf
            dis=[inf]*n
            dis[src]=0
            q=deque()
            q.append([src,-1])
            while q:
                i,fa=q.popleft()
                for j in g[i]:
                    if j==fa:
                        continue
                    if dis[j]!=inf:
                        cycle=min(cycle,dis[i]+dis[j]+1)
                    else:
                        dis[j]=dis[i]+1
                        q.append([j,i])
            return cycle
        
        ans=inf
        for i in range(n):
            ans=min(ans,bfs(i)) 
        bfs(1)
        if ans==inf:
            return -1
        
        return ans