LeetCode 2556. Disconnect Path in a Binary Matrix by at Most One Flip

February 6, 2023

雙周賽97。第三題想不出，剩下最後5分鐘發現這題比較簡單，沒時間做了。

題目

輸入m*n的二進位矩陣grid。你可以從(row, col)移動到(row + 1, col)或是(row, col + 1)，且其值為1的格子。若你無法從(0, 0)抵達(m - 1, n - 1)，則稱為不連通。

你可以將最多一個(也可能零個)格子的值翻面，但不可以翻(0, 0)和(m - 1, n - 1)。

如果你可以使得矩陣變成不連通，則回傳true，否則回傳false。

注意：將一個格子翻面會使得其值從0變成1，或是從1變成0。

解法

雖說0和1都可以翻面，但是把0翻成1不僅沒辦法使得路徑減少，反而有可能使得矩陣連通，因此只考慮把1翻成0。

最理想的狀況當然是矩陣本來就不連通。或是只有一條抵達的路徑，這樣無論如何，翻轉任意的1都可以使其不連通。
如果有兩條以上的不重疊路徑，不管切斷哪條，都會剩下其他條可以走，此矩陣將永遠連通。
那如果有多條路徑，但是都在某個點交會，是不是翻轉那個交會點就不連通了？

示意圖

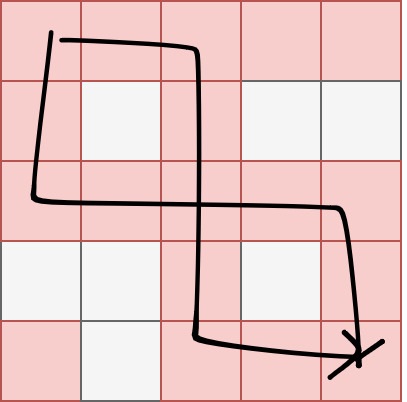
用想的很簡單，但是要怎麼找到這個關鍵點？
這種只能向下、向右走的題目有個關鍵點：總步數一定是M+N-2步。所以我們只要確保每一步中，有任一步不存在2種以上的可能位置，那就有可能成為不連通圖。

首先過濾掉無法抵達右下角的1，因為他們不會在任何有效路徑上。

示意圖

然後從起點開始dfs，每抵達一個新的位置，就將其對應的步數計數+1。
除了起點與終點以外，每個步數都應該至少存在2個以上的可能位置，所以從第1步檢查到M+N-3步。
若其中一步不符合，回傳true；否則代表存在多條路徑，回傳false。

時間複雜度O(M*N)。空間複雜度O(M*N)。

class Solution:
    def isPossibleToCutPath(self, grid: List[List[int]]) -> bool:
        M,N=len(grid),len(grid[0])
        ok=[0]*(M+N)
        
        for r in reversed(range(M)):
            for c in reversed(range(N)):
                if r==M-1 and c==N-1:continue
                if r==0 and c==0:continue
                down=r+1<M and grid[r+1][c]==1
                right=c+1<N and grid[r][c+1]==1
                if not down and not right:
                    grid[r][c]=0

        @cache
        def dfs(r,c):
            if r==M or c==N or grid[r][c]==0:
                return
            ok[r+c]+=1
            dfs(r+1,c)
            dfs(r,c+1)
        
        dfs(0,0)

        for i in range(1,M+N-2):
            if ok[i]<2:
                return True
            
        return False

另一種思路是：如果存在關鍵點，那麼刪除任意一條路徑必定也會刪除到關鍵點。

維護一個dfs(r,c)函數，代表從(r,c)出發是否能抵達右下角。在dfs的過程中把訪問過的1變成0，也就是刪除掉這條路徑。
注意：只能修改左上角和右下角以外的1，因為這兩點必定為1。

如果第一次dfs就失敗了，代表本來就沒連通，根本不用修改，直接回傳True。
否則，第一次dfs時已經刪掉連通一條路徑，再跑一次dfs確認是否連通。若不連通代表刪除到了關鍵點，回傳True；否則答案為False。

時間複雜度O(M*N)。直接修改grid，只需要遞迴的空間，空間複雜度O(M+N)。

class Solution:
    def isPossibleToCutPath(self, grid: List[List[int]]) -> bool:
        M,N=len(grid),len(grid[0])
        
        def dfs(r,c):
            if r==M or c==N or grid[r][c]==0:
                return False
            if r==M-1 and c==N-1:
                return True
            if r!=0 or c!=0:
                grid[r][c]=0
            return dfs(r+1,c) or dfs(r,c+1)
        
        # no connected
        if not dfs(0,0):
            return True

        # can disconnect
        if not dfs(0,0):
            return True

        return False

mocowcow

題目

解法