LeetCode 2364. Count Number of Bad Pairs

雙周賽84。個人覺得這題很妙，起初也是沒什麼頭緒，只好先跑去寫Q3才回來，最後靠著畫圖才想通。

題目

輸入整數陣列nums。如果i<j且j-i != nums[j]-nums[i]，則稱索引對(i, j)是錯誤的。
求nums中有多少錯誤的索引對。

解法

話不多說直接上圖。

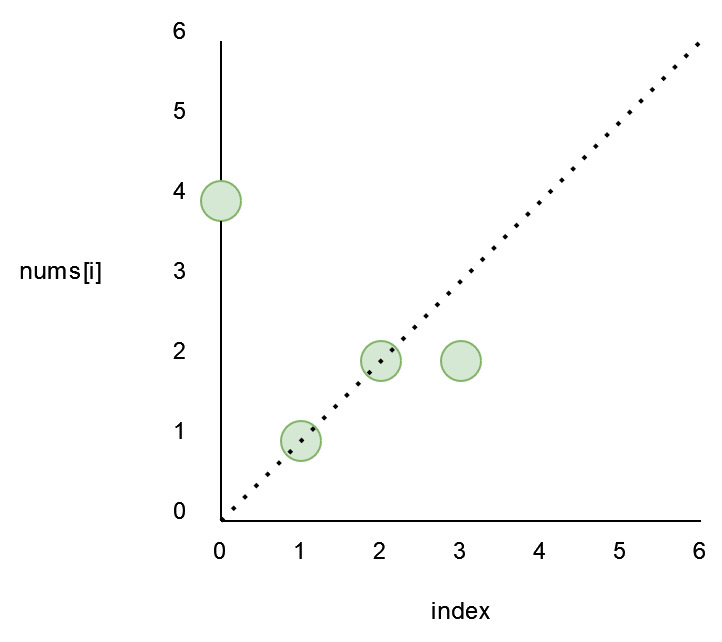
若j-i等於nums[j]-nums[i]，則i和j會在同一條斜率為1的直線上。可以透過i-nums[i]得到offset，作為斜線的編號。
維護雜湊表d，用來計算各協線上出現過多少個點。
遍歷的nums中的每個索引i和整數n，這時在n之前應該出現過正好i個點，其中有d[offset]個點是正確的，則得知剩下i-d[offset]個點可以和i組成錯誤的索引對，更新至答案中，最後將對應斜線的點計數+1。

class Solution:
    def countBadPairs(self, nums: List[int]) -> int:
        d=Counter()
        ans=0
        
        for i,n in enumerate(nums):
            offset=i-n
            ans+=i-d[offset]
            d[offset]+=1
        
        return ans

看了別人的想法，發現我終究是繞了遠路，根本不用畫圖。
只要把不等式移項就一目了然：

j-i != nums[j]-nums[i]
j-nums[j] != i-nums[i]

題目直接簡化成找到j-nums[j] != i-nums[i]的索引對數。
也可以預先計算出所有索引對數量，在遍歷過程中刪除正確的索引對，最後只會剩下錯誤的索引對。

class Solution:
    def countBadPairs(self, nums: List[int]) -> int:
        N=len(nums)
        total=N*(N-1)//2
        good=0
        d=Counter()
        
        for i,n in enumerate(nums):
            offset=i-n
            good+=d[offset]
            d[offset]+=1
        
        return total-good