LeetCode 2322. Minimum Score After Removals on a Tree

June 28, 2022

周賽299。看就想到樹狀dp，但不知道怎麼表達切開的子樹。一直想著要怎麼在dfs函數上處理切割第幾刀，整個思路都是錯的。
說起來這兩次周賽都完全沒出bug，雖然都沒做出Q4，但排名還算前面，算挺開心的。

題目

有一顆無向的樹，由n個節點和n-1個邊所組成。
輸入長度n的陣列nums，其中nums[i]代表第i個節點的值。還有長度n-1的二維陣列edges，其中edges[i] = [ai, bi]，代表連接兩點的邊。

你必須移除兩條不同的邊，使這棵樹變成三個部分，並計算出分數：

對於每個部份，將相連的節點全部做XOR運算
計算出的三個結果中，最大值和最小值的差即為該分割法的分數

求所有切割方法中，分數最小可以為多少。

解法

參考這篇文章的解法，差別在於我使用dfs而非bfs。
任選一點作為樹的root，用dfs得到每個子樹的總XOR值，並維護每個子樹的子節點來判斷分割部分的相對位置。

因方便起見，總是選擇節點0作為整棵樹的root。
維護陣列v代表各子樹的XOR值，集合陣列c代表各子樹的所有子節點。
從0開始對所有子節點做dfs，再將子節點的XOR值和子節點更新到當前節點上。

再來列舉所有切割的方式，切成三塊後，只會有三種狀況：

第一刀在第二刀的子樹中
第二刀在第一刀的子樹中
兩刀各產生一個子樹

示意圖

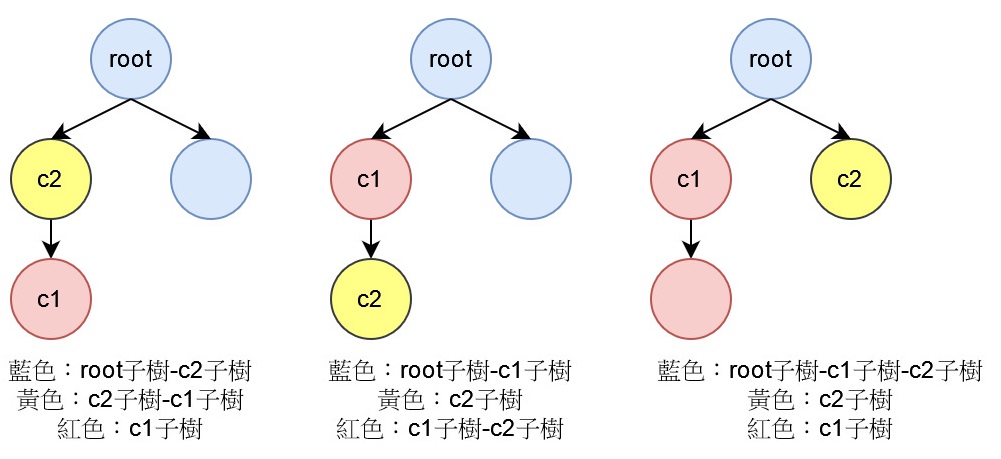
先判斷邊上兩點，哪一點是子節點，再以兩個子節點c1和c2判斷父子關係。
若c1存在於c2的子樹中，則是第一種情況；c2存在於c1子樹中，第二種情況；剩下就是第三種。

class Solution:
    def minimumScore(self, nums: List[int], edges: List[List[int]]) -> int:
        N=len(nums)
        v=nums[:]
        c=[set() for _ in range(N)]
        ans=inf
        g=defaultdict(list)
        for a,b in edges:
            g[a].append(b)
            g[b].append(a)
            
        def dfs(i,prev):
            for adj in g[i]:
                if adj==prev:continue
                v[i]^=dfs(adj,i)
                c[i]|={adj}|c[adj]
            return v[i]
        
        dfs(0,None)
        
        def getChild(i):
            a,b=edges[i]
            if a in c[b]:
                return a
            return b
       
        for i in range(N-1):
            c1=getChild(i)
            for j in range(N-1):
                c2=getChild(j)
                if c1 in c[c2]:#c1 down
                    g1=v[c1]
                    g2=v[c1]^v[c2]
                    g3=v[0]^v[c2]
                elif c2 in c[c1]:#c2 down
                    g1=v[c2]
                    g2=v[c1]^v[c2]
                    g3=v[0]^v[c1]
                else:
                    g1=v[c1]
                    g2=v[c2]
                    g3=v[0]^g1^g2
                    
                ans=min(ans,max(g1,g2,g3)-min(g1,g2,g3))
            
        return ans

這篇文提供另一種判斷子樹關係的方法，叫做時間戳(timestamp)。在dfs的過程中，紀錄每個子樹的進入時間，以及離開時間。

維護長度N的陣列tin和tout，代表每個子樹的進入時間戳，以及離開時間戳。
dfs每進入一個新節點時，timestamp遞增一。然後更新tin，對所有子節點遞迴，最後才更新tout。

示意圖

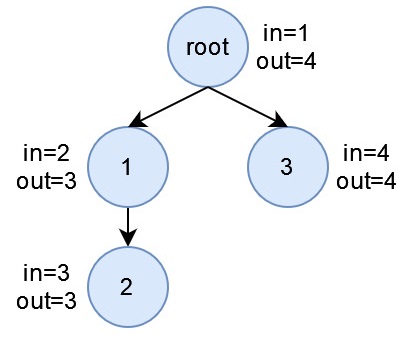
根據dfs的特性，當我們處理節點i時，一定會先遞迴處理完i的所有子節點，之後才離開i。
因此，若某節點j為i的子孫節點，則[j進入時間點, j離開時間點]一定會被[i進入時間點, i離開時間點]所完全包含。

不同於上面列舉邊的方法，這裡必須改成列舉不同的兩個點。
將子樹切成三部分，第一個部分一定是以root為根節點的子樹，而列舉的另外兩個節點則為剩下的兩棵子樹。
因為root節點0一定會使用到，所以從1開始列舉到N-1。

class Solution:
    def minimumScore(self, nums: List[int], edges: List[List[int]]) -> int:
        N=len(nums)
        v=nums[:]
        tin=[0]*N
        tout=[0]*N
        timestamp=0
        ans=inf
        g=defaultdict(list)
        for a,b in edges:
            g[a].append(b)
            g[b].append(a)
            
        def dfs(i,prev):
            nonlocal timestamp
            timestamp+=1
            tin[i]=timestamp
            for adj in g[i]:
                if adj==prev:continue
                v[i]^=dfs(adj,i)
            tout[i]=timestamp
            return v[i]
        
        dfs(0,None)
       
        for i in range(1,N):
            for j in range(i+1,N):
                if tin[i]<=tin[j]<=tout[j]<=tout[i]: # i is parent
                    g1=v[0]^v[i]
                    g2=v[i]^v[j]
                    g3=v[j]
                elif tin[j]<=tin[i]<=tout[i]<=tout[j]: # j is parent
                    g1=v[0]^v[j]
                    g2=v[j]^v[i]
                    g3=v[i]
                else:
                    g1=v[0]^v[i]^v[j]
                    g2=v[i]
                    g3=v[j]
                ans=min(ans,max(g1,g2,g3)-min(g1,g2,g3))
            
        # print(c)
        # print(v)
        return ans

mocowcow

題目

解法