LeetCode 2183. Count Array Pairs Divisible by K

模擬周賽281。有夠抽象的腦筋急轉彎，數學底子好真的是秒殺。

題目

商入長度為n的陣列nums和整數k，求符合以下條件的數對(i,j)有多少：

• i和j介於0和n-1間，且i<j
• nums[i]*nums[j]被k整除

解法

n最大可以到10^5，雙迴圈暴力法就不用嘗試了，一定不會過。

(a*b)若要被k整除，必須是k的倍數，但是要怎麼確定是不是k的倍數？
先想像把每個數字做質因數分解，任選兩個數，其總和若滿足k的質因數數量，則保證能夠整除：

a=[2*2], b=[3*3], k=[2*3]
(a*b)=[2*2*3*3] 故可以被k整除

但是為了方便計算，所以我們直接取n和k的最大公因數，即把不需要的因數砍掉，如圖：

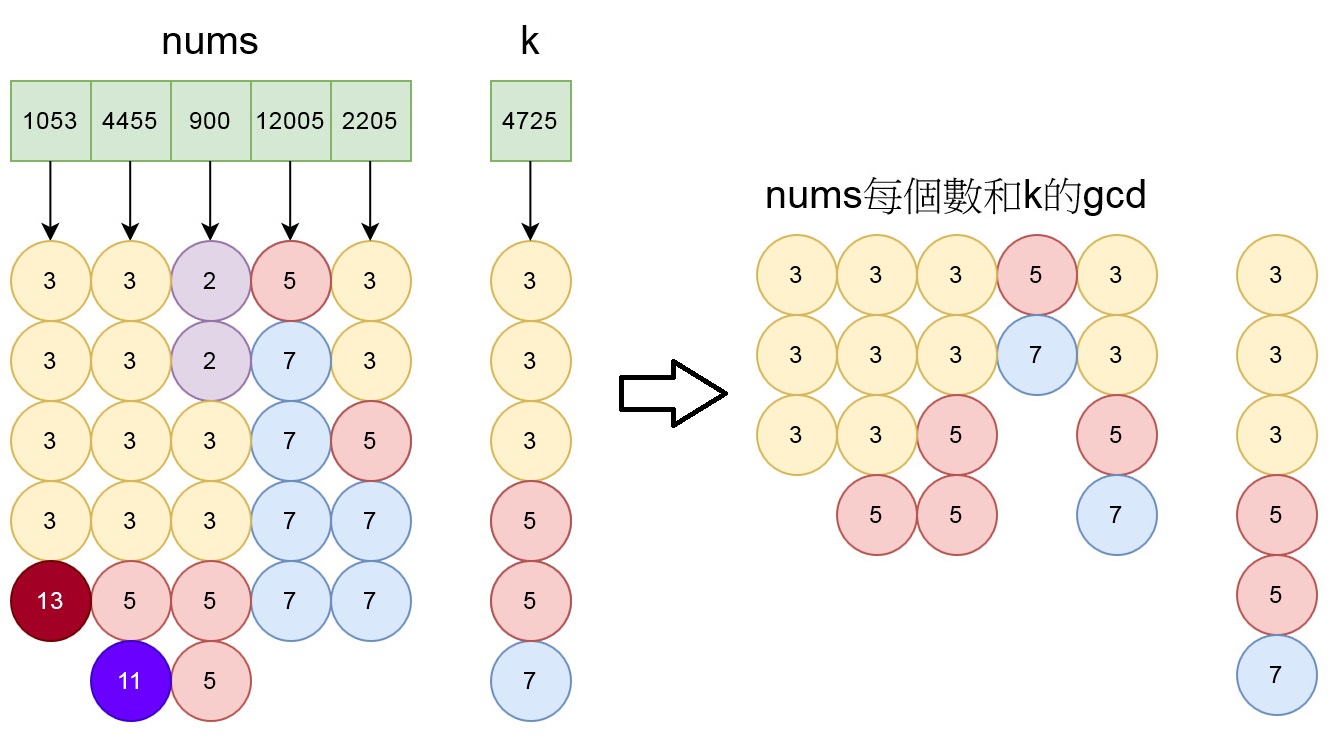
這樣一來，就可以將所有數字做等價轉換，裝進雜湊表計數，降低複雜度。
遍歷nums中每個數nums[j]，對雜湊表d中每個key相乘，看是否能被k整除。若能整除，則答案增加d[key]種。最後將以gcd(nums[j],k)計數加1。

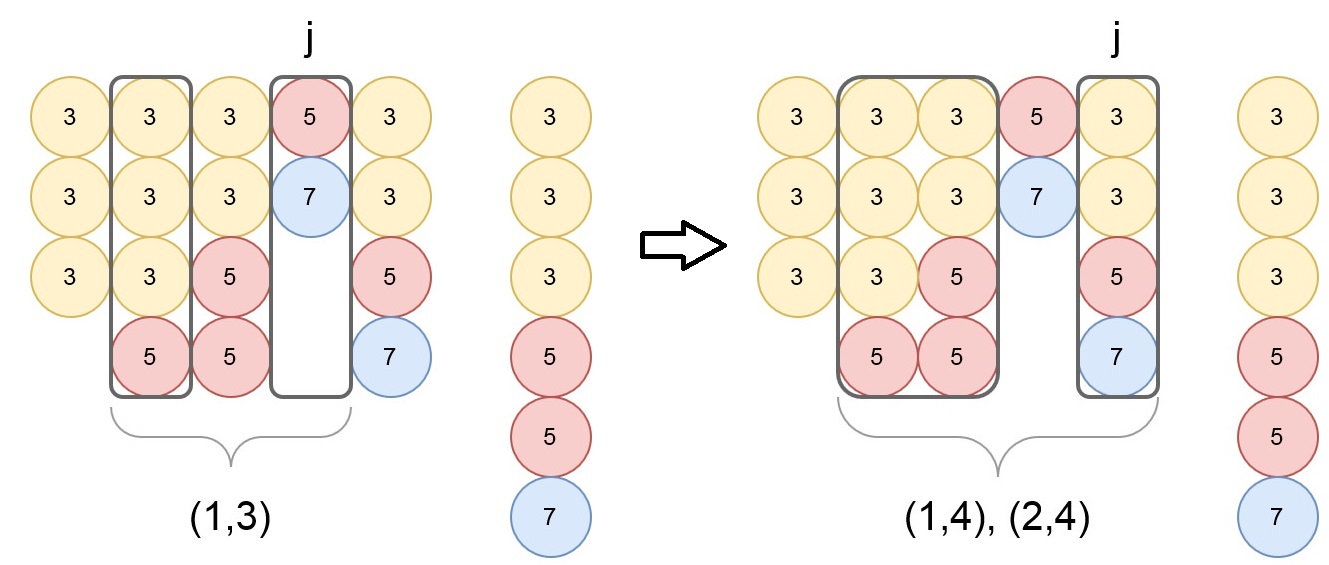
class Solution:
    def countPairs(self, nums: List[int], k: int) -> int:
        d=defaultdict(int)
        ans=0
        for n in nums:
            x=math.gcd(n,k)
            for key,v in d.items():
                if (key*x)%k==0:
                    ans+=v
            d[x]+=1
                
        return ans