LeetCode 2179. Count Good Triplets in an Array

模擬雙周賽72。一開始還真是完全摸不著頭緒，看了滿多篇解答，不是解釋不清楚，就是刻意寫得很艱深，連集合論的bijection都拿出來講，好險最後是有看到幾篇正常的。

題目

輸入兩個長度為N個陣列nums1, nums2，他們都是[0,1,..,n-1]的排列。
一個好的三元組是一組三個不同的值，以相同的順序出現在nums1和nums2中。
例：

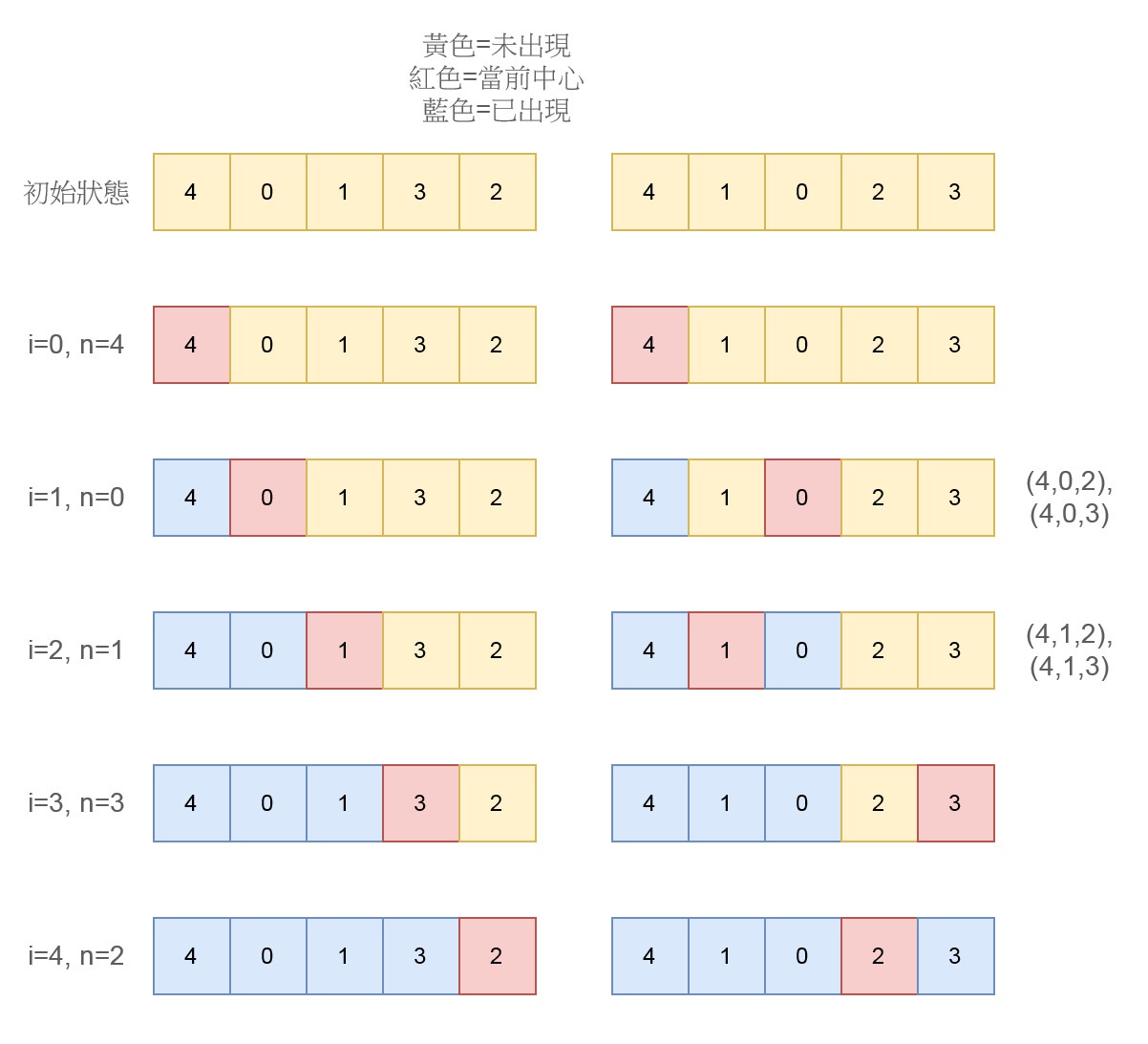
nums1 = [4,0,1,3,2], nums2 = [4,1,0,2,3]
有四個好的三元組
(4,0,3), (4,0,2), (4,1,3) 和 (4,1,2)

解法

同時處理兩邊的出現順序太麻煩了，可以先用雜湊表記錄下nums2裡面各元素的索引位置。
如此一來，我們只需要枚舉nums1的所有元素n做為中間元素，計算nums中n的左方元素有那些已經出現過、n的右方元素有哪些還沒出現過，就可以得到以n為中間點的組合數量。

最後問題剩下要用什麼資料結構，才能快速查詢區間和？線段樹、BIT或是sorted list。
附上助我良多的優質題解。

class BinaryIndexedTree:
    def __init__(self, n):
        self.bit = [0]*(n+1)
        self.N = len(self.bit)

    def update(self, index, val):
        index += 1
        while index < self.N:
            self.bit[index] += val
            index = index + (index & -index)

    def prefixSum(self, index):
        index += 1
        res = 0
        while index > 0:
            res += self.bit[index]
            index = index - (index & -index)
        return res

class Solution:
    def goodTriplets(self, nums1: List[int], nums2: List[int]) -> int:
        d={x:i for i,x in enumerate(nums2)}
        N=len(nums1)
        bit=BinaryIndexedTree(N+5)
        ans=0
        for i,n in enumerate(nums1):
            x=d[n]
            lsmall=bit.prefixSum(x-1)
            rbig=N-1-x-(i-lsmall)
            ans+=lsmall*rbig
            bit.update(x,1)
            
        return ans

不用BIT，改拿sorted list偷雞，還快了不少。

from sortedcontainers import SortedList

class Solution:
    def goodTriplets(self, nums1: List[int], nums2: List[int]) -> int:
        d={x:i for i,x in enumerate(nums2)}
        N=len(nums1)
        ans=0
        sl=SortedList()
        for i,n in enumerate(nums1):
            x=d[n]
            left=sl.bisect_left(x)
            right=N-1-x-(i-left)
            ans+=left*right
            sl.add(x)
            
        return ans