LeetCode 2127. Maximum Employees to Be Invited to a Meeting

October 3, 2023

還挺好玩的拓圖排序題，而且範例給的很充足。

題目

公司要開一場會議，名單上有n個員工被邀請參加。他們會坐在一個圓形桌上，桌子可以容納所有人。

員工編號分別從0到n-1。每個員工都有其最愛的人，且只有能坐那人旁邊時才願意出席會議。最愛的人不會是自己。

輸入整數陣列favorite，其中favorite[i]是第i個員工最愛的人。
求最多能夠讓幾個人出席會議。

解法

n個人，n條邊，一定會有循環。循環內的所有人必須一起出席。

最單純的情況就是範例2，整群人頭尾相接的圓圈。
這種情況下沒有任何空間容得下外人。

複雜一點如範例1，環上只由兩人組成，他們互相滿足，這時可以允許兩人各帶著一條單向喜歡的粉絲隊伍。
例如：

1 > 2 > 3 <> 4 < 5
ans = 5

3和4互相喜歡，但是3另外帶了兩個人，4也多帶一個人。
位於最外圈的1和5都被滿足了。這種基於大小2環的結構同時出現多個，例如：

1 <> 2 + 3 <> 4

示意圖

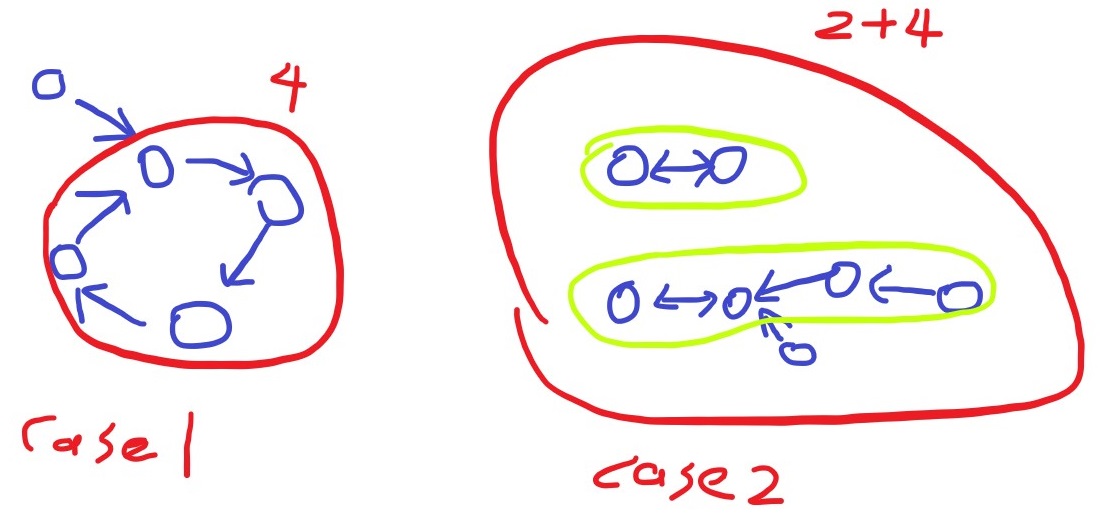
所以我們只要找出所有環，並根據環的大小分類討論：

環大小為2，找到兩人最長的單向粉絲隊伍，將總人數累計
環大小為3以上，只能有這個環，更新最大單環大小

一坨小環組成的小團體，或是一個大環，取較大者就是答案。

先拓樸排序，把所有葉節點刪掉，剩下的節點一定位於某個環中。
對favorite建立逆向圖，也就是紀錄父節點。在找出環上所有節點後，從環開始逆向bfs/dfs找回去，找到最長的粉絲隊伍。
最後根據環的大小決定是小環還是大環。

時間複雜度O(N)。
空間複雜度O(N)。

class Solution:
    def maximumInvitations(self, favorite: List[int]) -> int:
        g=favorite
        N=len(g)
        rev=[[] for _ in range(N)]
        ind=[0]*N
        
        for i,x in enumerate(g):
            ind[x]+=1
            rev[x].append(i)
            
        q=deque()
        for i,x in enumerate(ind):
            if x==0:
                q.append(i)
                
        while q:
            i=q.popleft()
            j=g[i]
            ind[j]-=1
            if ind[j]==0:
                q.append(j)
        
        part=0
        big=0
        for i in range(N):
            if ind[i]<=0:
                continue
            
            ring=[]
            curr=i
            while True:
                ring.append(curr)
                ind[curr]=-1
                curr=g[curr]
                if curr==i:
                    break
            
            def dfs(i):
                res=0
                for j in rev[i]:
                    if ind[j]==0:
                        res=max(res,dfs(j)+1)
                return res
            
            size=len(ring)
            if size==2:
                part+=size+dfs(i)+dfs(g[i])
            else:
                big=max(big,size)
        
        return max(part,big)

mocowcow

題目

解法