LeetCode 1738. Find Kth Largest XOR Coordinate Value

August 31, 2022

隨便抽到的題。算是2D前綴和的變種題，但是有一些可以優化的小地方。

題目

輸入m*n的矩陣，由非負整數組成，還有一個整數k。
產生另一個矩陣，其座標(a,b)的值為所有matrix[i][j]的XOR結果，其中0<=i<=a<m且0<=j<=b<n。

找到矩陣中第k大的值。

解法

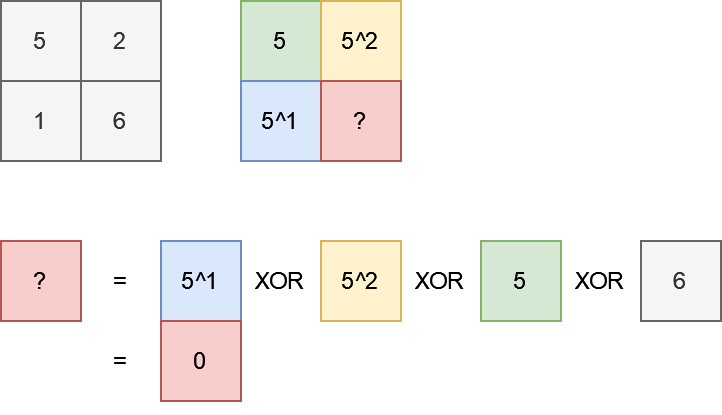
中心思想和304. range sum query 2d immutable一樣，由四個區域來計算出當前的總和。
差別在於XOR的特性，相同的數字會相消，所以四個區塊互相做XOR就好。
計算出每個位置的XOR總和之後，排序並回傳第k大的值。

示意圖

XOR總和矩陣的複雜度為O(M*N)，共有MN個元素。排序複雜度為O(MN log MN)，整體複雜度為O(MN log MN)。

class Solution:
    def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:
        M,N=len(matrix),len(matrix[0])
        dp=[[0]*N for _ in range(M)]
             
        for r in range(M):
            for c in range(N):
                up=0 if r==0 else dp[r-1][c]
                left=0 if c==0 else dp[r][c-1]
                upleft=0 if (c==0 or r==0) else dp[r-1][c-1]
                dp[r][c]=up^left^upleft^matrix[r][c]
                        
        return sorted(dp[r][c] for r in range(M) for c in range(N))[-k]

可以使用min heap代替排序，只維護k個最大的元素，將複雜度將低到O(M*N log k)。
在產生XOR總和的過程中只保留大的k個元素，如果新加入的值後超過k個，則彈出最小的。如此一來heap頂端將會是第k大的總和，因為M*N個更小的元素已經被刪掉了。

class Solution:
    def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:
        M,N=len(matrix),len(matrix[0])
        dp=[[0]*N for _ in range(M)]
        h=[]
             
        for r in range(M):
            for c in range(N):
                up=0 if r==0 else dp[r-1][c]
                left=0 if c==0 else dp[r][c-1]
                upleft=0 if (c==0 or r==0) else dp[r-1][c-1]
                dp[r][c]=up^left^upleft^matrix[r][c]
                if len(h)==k:
                    heappushpop(h,dp[r][c])
                else:
                    heappush(h,dp[r][c])
                        
        return h[0]

看到別人有更簡單的做法，雖然複雜度一樣是O(MN log k)，但是實作起來方便很多。
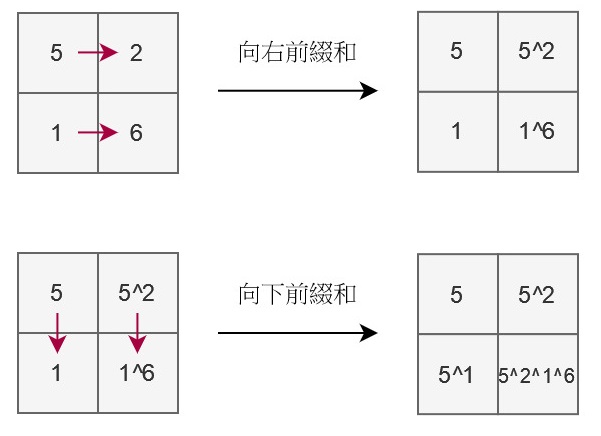
先遍歷每一列，向右方做前綴和(前綴XOR?)。再遍歷每一行，往下方最前綴和，這樣正好是對於所有元素都做一次XOR。
最後一樣使用heap找出第k大的元素。

示意圖

class Solution:
    def kthLargestValue(self, matrix: List[List[int]], k: int) -> int:
        M,N=len(matrix),len(matrix[0])
        h=[]
             
        for r in range(M):
            for c in range(1,N):
                matrix[r][c]^=matrix[r][c-1]
                    
        for c in range(N):
            for r in range(1,M):
                matrix[r][c]^=matrix[r-1][c]
                    
        for r in range(M):
            for c in range(N):
                if len(h)==k:
                    heappushpop(h,matrix[r][c])
                else:
                    heappush(h,matrix[r][c])
                        
        return h[0]

mocowcow

題目

解法