LeetCode 1329. Sort the Matrix Diagonally

每日題。好像沒什麼太多的作法可以選擇，倒是很適合練習計算複雜度。

題目

輸入M*N的矩陣mat，將處在同一條右斜對角線上的元素重新排列，將較小的元素放在較上方的列。

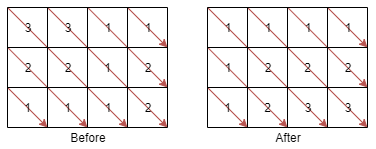
解法

位於同一條右斜對角線上的元素，其列數r扣掉行數c會得到相同的值。

維護雜湊表，遍歷所有元素mat[r][c]，計算出對角線值r-c作為索引，將元素加入雜湊表中。
將所有對角線中的元素依遞減排序，方便之後作為堆疊使用。
再次遍歷所有元素mat[r][c]，但這次只要從對應的對角線中取值寫入即可。先前將元素遞減排序，所以頂端元素會是最小值，取出頂端元素賦值即可。

總共會產生M+N-1條對角線，每條最多min(M,N)=k個元素。遍歷矩陣兩次的複雜度為O(M*N)，排序所有對角線複雜度為O((M+N)k log k)。
參考自這篇文，又因(M+N)k約等於M*N，所以O((M+N)k log k)可以化簡為O(MN log k)。

class Solution:
    def diagonalSort(self, mat: List[List[int]]) -> List[List[int]]:
        M,N=len(mat),len(mat[0])
        d=defaultdict(list)
        
        for r in range(M):
            for c in range(N):
                d[r-c].append(mat[r][c])
                
        for k in d:
            d[k].sort(reverse=True)
            
        for r in range(M):
            for c in range(N):
                mat[r][c]=d[r-c].pop()
                
        return mat