LeetCode 1245. Tree Diameter

July 6, 2024

上次周賽有用到樹的直徑，趁機會補一下題解。

題目

樹的直徑指的是樹中最長路徑的邊數。

有一個 n 節點的無向樹，編號分別從 0 到 n - 1。
輸入二維整數陣列 edges，其中 edges[i] = [a_i, b_i]，代表 a_i 和 b_i 之間存在一條邊。

求樹的直徑。

解法

無向樹其實是一種無向圖，可以任意選擇節點做樹根。
想通這點後清晰很多。

本題固定選擇 0 做為根節點。

直徑是必定是由兩個節點所組成的最長路徑，有可能是：

根節點出發，走到某個葉節點
某個葉節點出發，走到另一個葉節點

考慮每個節點做為子樹時，與直徑的關係：

直徑在當前節點轉彎。子樹中兩條最長路徑構成直徑
直徑不在當前節點轉彎。而是由最長的一條，在更上層的位置才轉彎

因此我們在求每個子樹的最大深度時，可以順便透過兩條最大深度來更新直徑，並回傳最大深度，供祖先節點使用。

時間複雜度 O(N)。
空間複雜度 O(N)。

class Solution:
    def treeDiameter(self, edges: List[List[int]]) -> int:
        N = len(edges) + 1
        g = [[] for _ in range(N)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)

        res = 0
        def dp(i, fa):
            nonlocal res
            mx1 = mx2 = 0
            for j in g[i]:
                if j == fa:
                    continue
                t = dp(j, i)
                if t > mx1:
                    mx1, mx2 = t, mx1
                elif t > mx2:
                    mx2 = t
            res = max(res, mx1 + mx2) # update diameter
            return mx1 + 1 # max depth

        dp(0, -1)
        
        return res

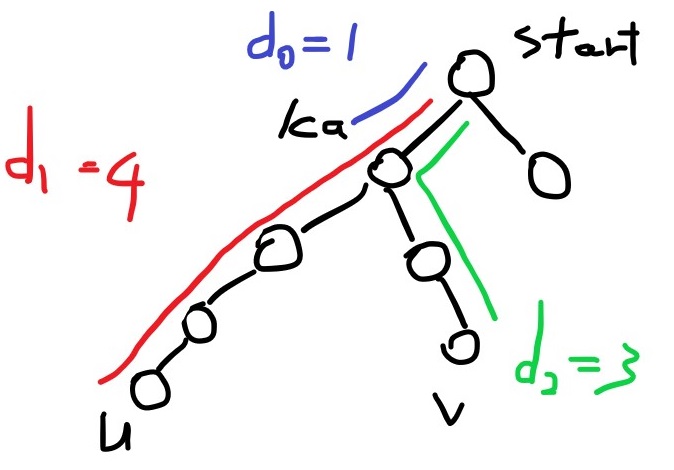
直徑 (u, v) 是由兩個距離最遠的節點構成。
從任意節點出發，找到的最遠節點必定是直徑的一端 u。
然後從 u 出發，再次找到的最遠節點 v 便是另一端。

(u, v) 兩點的距離即為直徑。

在此之前，需要證明任意點的最遠端點必為直徑端點。

記得，樹狀圖是可以隨意調整樹根的，為方便思考討論，則將出發點 start 設為樹根。
而 u, v 與出發點的距離 d1 = (start, u), d2 = (start, v)，且滿足 d1 >= d2。
u, v 的共通祖先記做 lca，與出發點的距離記做 d0 = (start, lca)。
則直徑公式為：

diameter = (u, v) = d1 + d2 - (d0) * 2

如下圖所示：
示意圖

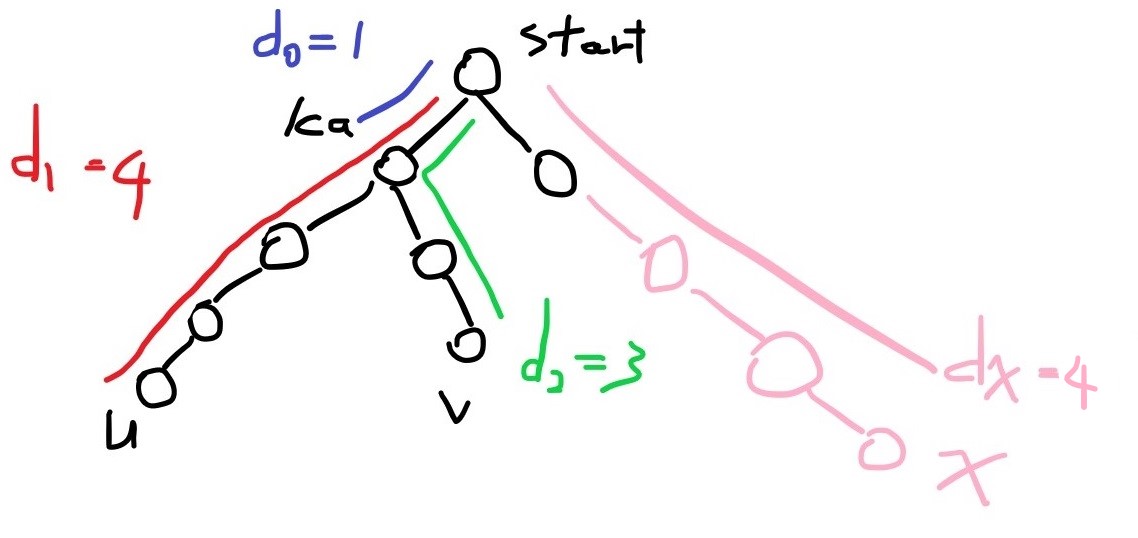
假設存在某節點 x，其距離 dx 等於 d1，但 x 不屬於 u 或 v。
可以把 u 或 v 替換成 x，得到比 (u, v) 更長的距離，與 (u, v) 為直徑的前提矛盾。

示意圖

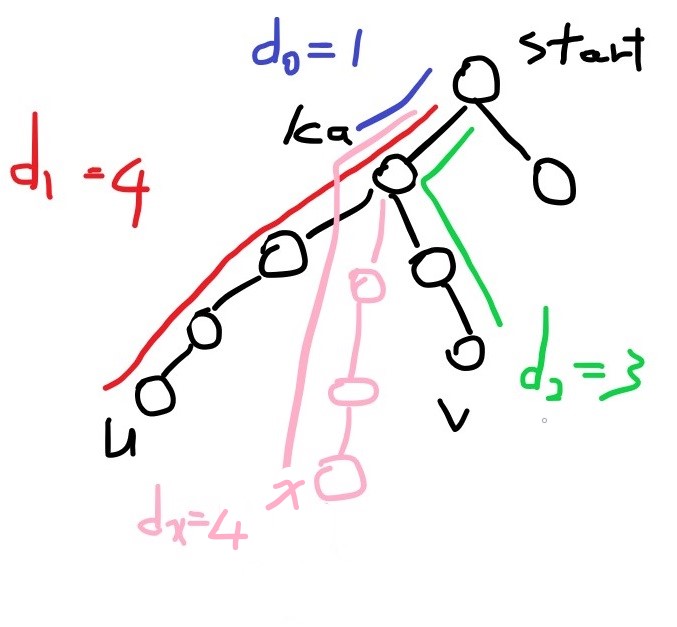
綜上所述，只要透過 dfs/bfs 尋找最遠點的算法，就可以間接求出直徑。

時間複雜度 O(N)。
空間複雜度 O(N)。

class Solution:
    def treeDiameter(self, edges: List[List[int]]) -> int:
        return diameter_dfs(edges) # diameter_bfs(edges)

def diameter_dfs(edges):
    N = len(edges) + 1
    g = [[] for _ in range(N)]
    for a, b in edges:
        g[a].append(b)
        g[b].append(a)

    farthest = None
    mx_dist = -1

    def dfs(i, fa, dist):
        nonlocal farthest, mx_dist
        if dist > mx_dist:
            mx_dist = dist
            farthest = i
        for j in g[i]:
            if j == fa:
                continue
            dfs(j, i, dist + 1)

    dfs(0, -1, 0)

    mx_dist = -1
    dfs(farthest, -1, 0)
    return mx_dist

def diameter_bfs(edges):
    N = len(edges) + 1
    g = [[] for _ in range(N)]
    for a, b in edges:
        g[a].append(b)
        g[b].append(a)

    def bfs(start):
        dist = [-1] * N
        dist[start] = 0
        q = [start]
        while q:
            q2 = []
            for i in q:
                for j in g[i]:
                    if dist[j] == -1:
                        dist[j] = dist[i] + 1
                        q2.append(j)
            q = q2

        farthest = None
        mx_dist = -1
        for i, d in enumerate(dist):
            if d > mx_dist:
                mx_dist = d
                farthest = i
        return farthest, mx_dist

    u, dist = bfs(0)
    v, dist = bfs(u)
    return dist

把樹狀圖當作洋蔥，最外層的點指向內層的點，分成好幾層。
可以像剝洋蔥一樣，每次拔掉最外面那層，直到剩下核心為止。
剝皮次數只和直徑相關，每次剝皮會使直徑減少 2。

示意圖

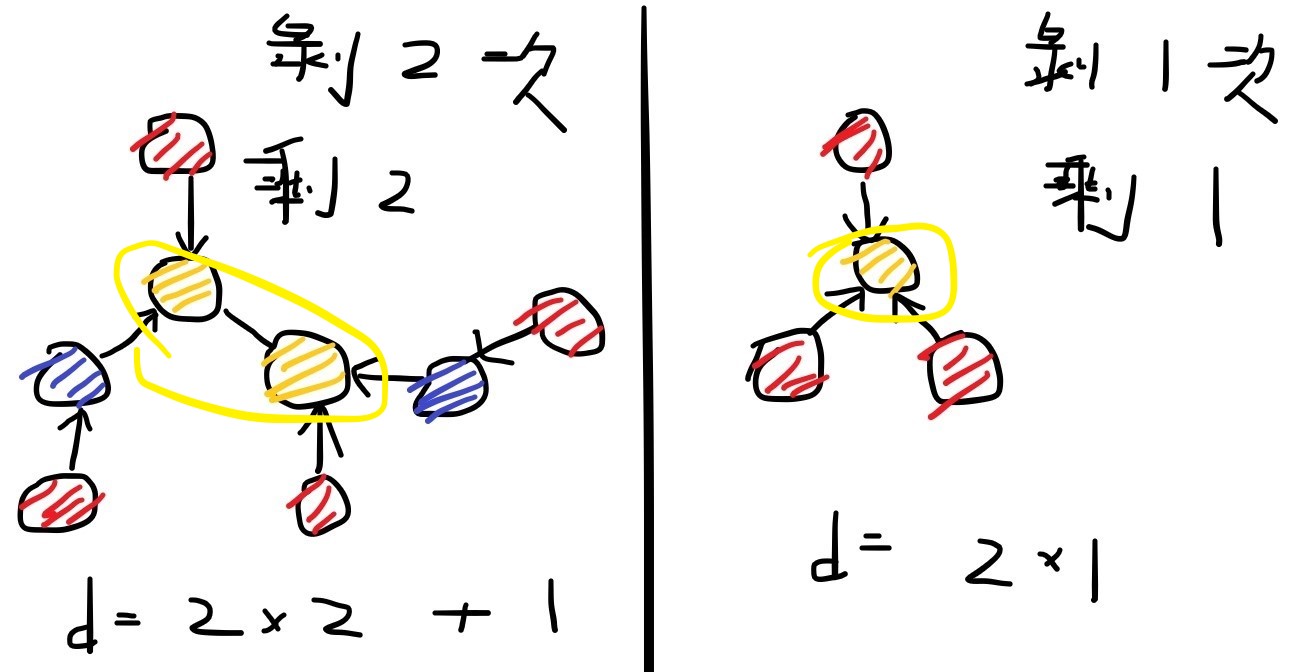
注意核心有兩種可能：

剩 1 個節點，不影響直徑
剩 2 個節點，直徑多 1

答案即為剝皮次數 * 2 + 核心產生的距離。

class Solution:
    def treeDiameter(self, edges: List[List[int]]) -> int:
        return diameter_topology_sort(edges)

def diameter_topology_sort(edges):
    N = len(edges) + 1

    if N <= 2:
        return N - 1

    g = [[] for _ in range(N)]
    indegree = [0] * N
    for a, b in edges:
        g[a].append(b)
        g[b].append(a)
        indegree[a] += 1
        indegree[b] += 1

    q = []
    for i in range(N):
        if indegree[i] == 1:
            q.append(i)

    remain = N
    dist = 0
    while remain > 2:
        dist += 1
        q2 = []
        for i in q:
            remain -= 1
            for j in g[i]:
                indegree[j] -= 1
                if indegree[j] == 1:
                    q2.append(j)
        q = q2

    diameter = dist * 2
    if remain == 2:
        diameter += 1
    return diameter

mocowcow

題目

解法