LeetCode 1183. Maximum Number of Ones

每周會員題。雖然以前是免費題，突然變成付費題，好慘。

題目

有個width * height的矩陣M，只由0或1組成。其中所有sideLength * sideLength的子陣列之中最多只包含maxOnes個1。

求M裡面最多可以多有少1。

解法

首先考慮side*side，左上角為(0,0)的子矩陣，假設我們向右偏移一格，則原本第一行會變成新矩陣最後一行；同理，向下偏移，原本第一列會會成為新矩陣的最後一列。

例如：

[[1,2],[3,4]]
若往右偏移變成[[2,1],[4,3]]
若往下偏移變成[[3,4],[1,2]]

換句話說，對於格子(r,c)來說，所有(r%sideLength, c%sideLength)相等的格子都會是相同的值。

當M是10 * 10，且sideLength為4時，分布如下。每個子矩陣都是由編號1~16的格子所組成。

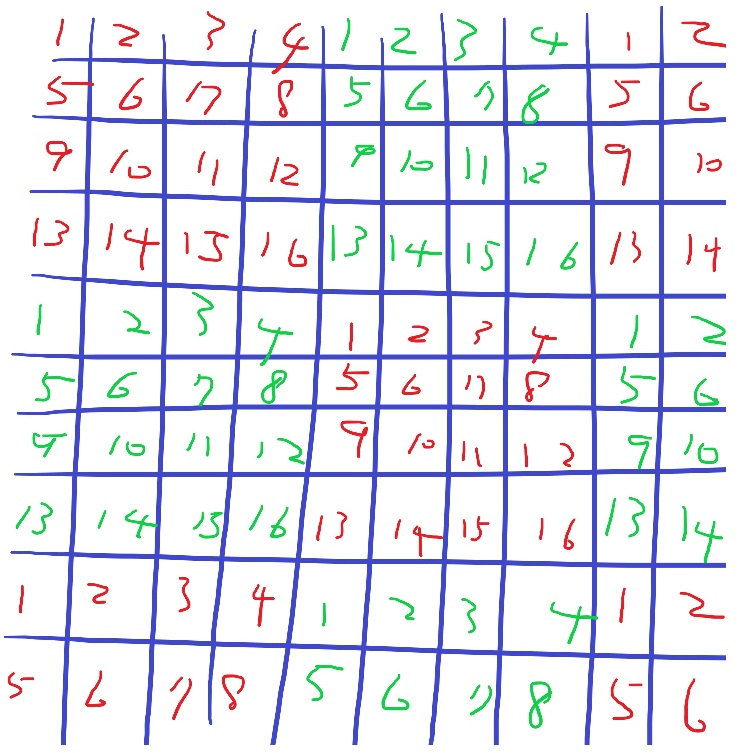
其中編號1,2,5,6各出現了9次，11,12,15,16各出現4次，其於編號各出現6次。
我們需要做的，就是在這16的編號中選擇k個填上1。但每個編號出現次數不同，所以優先選擇頻率最高的k個。

總共有ID = sideLength^2個獨特的編號，按照編號計數後以頻率排序。
時間複雜度O(width*height + ID log ID)。
空間複雜度O(ID)。

class Solution:
    def maximumNumberOfOnes(self, width: int, height: int, sideLength: int, maxOnes: int) -> int:
        d=Counter()
        
        for r in range(height):
            x=r%sideLength
            for c in range(width):
                y=c%sideLength
                d[(x,y)]+=1
                
        a=sorted(d.values(),reverse=True)
        
        return sum(a[:maxOnes])