LeetCode 1129. Shortest Path with Alternating Colors

March 9, 2022

臭狗拿完心臟藥回來不吃東西，結果是牙痛，拿完止痛藥又四肢無力顫抖。希望他能不再痛苦。

題目

一個有向圖，共n個節點。redEdges代表紅色單向路段，blueEdges代表藍色單向路段，且只能紅藍交替著走。回傳answer陣列，answer[i]代表0出發開始到每i最少需要幾步，若無法到達則為-1。

解法

分別建立兩個有向圖gRed, gBlue表示表示紅藍路線。
從起點0出發時，可以選紅或藍，之後就必須不斷交替了。一開始我把BFS函數化，分別算紅出發與藍出發的各點距離，最後合併結果，但是碰到了這種特例就爆炸了：

redEdges : [[0,1],[1,2],[2,3],[3,4]]
blueEdges : [[1,2],[2,3],[3,1]]

示意圖
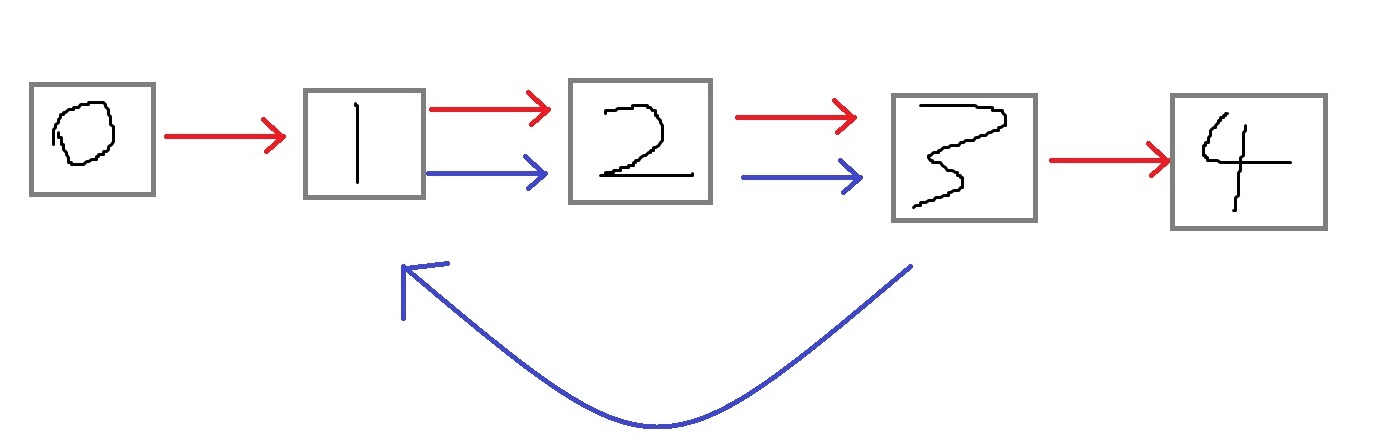
照上述做法的話，紅出發只能到0,1,2,3，因3~4只有紅色，無法再走了。而藍出發根本出不去。可是正確答案為[0,1,2,3,7]，我才發現有可能回到原來的點，但是走不同顏色。

那麼只好同時維護兩種顏色路線的距離，一起做BFS。數對(x,color)，x為目前點，color=0代表紅色，而1代表藍色，每次移動後都會交換。邊走邊依照對應的陣列更新最短距離，一樣在最後倆倆合併為answer即可。

class Solution:
    def shortestAlternatingPaths(self, n: int, redEdges: List[List[int]], blueEdges: List[List[int]]) -> List[int]:
        gRed = defaultdict(list)
        gBlue = defaultdict(list)
        for a, b in redEdges:
            gRed[a].append(b)
        for a, b in blueEdges:
            gBlue[a].append(b)

        dRed = [math.inf]*n
        dBlue = [math.inf]*n
        step = 0
        q = [(0, 0), (0, 1)]  # 0:red, 1:blue
        while q:
            t = []
            for x, color in q:
                if color == 0:
                    dist = dRed
                    g = gRed
                else:
                    dist = dBlue
                    g = gBlue
                if step >= dist[x]:
                    continue
                dist[x] = step
                for adj in g[x]:
                    t.append((adj, color ^ 1))
            q = t
            step += 1

        ans = []
        for a, b in zip(dBlue, dRed):
            if math.inf == a == b:
                ans.append(-1)
            else:
                ans.append(min(a, b))

        return ans

mocowcow

題目

解法