LeetCode 1074. Number of Submatrices That Sum to Target

每日題。看到題目時非常開心，以為是2D前綴和模板題，從函數庫貼一貼送出答案，拿到免費的TLE。

題目

輸入矩陣matrix和整數target，回傳總和為target的子矩陣數量。

解法

本來想說建個2D前綴和，然後列舉全部的子矩陣，若符合target答案就+1。
每個矩陣有四格座標，共需要四個迴圈，整體複雜度為O(N^2*M^2)，可惜M和N上限為100，帶入後大約需要10^8次運算，不太可能通過的。如果M和N都只有50的話，搞不好還有機會。

class PrefixSum2D:
    def __init__(self, matrix):
        M, N = len(matrix), len(matrix[0])
        self.psum = [[0]*(N+1) for _ in range(M+1)]
        for r in range(M):
            for c in range(N):
                self.psum[r+1][c+1] = self.psum[r][c+1] + \
                    self.psum[r+1][c]-self.psum[r][c]+matrix[r][c]

    def rangeSum(self, r1, c1, r2, c2):
        return self.psum[r2+1][c2+1]-self.psum[r2+1][c1]-self.psum[r1][c2+1]+self.psum[r1][c1]
    
class Solution:
    def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
        M,N=len(matrix),len(matrix[0])
        ps=PrefixSum2D(matrix)
        ans=0
        for x1 in range(M):
            for x2 in range(x1,M):
                for y1 in range(N):
                    for y2 in range(y1,N):
                        if ps.rangeSum(x1,y1,x2,y2)==target:
                            ans+=1
                            
        return ans

提示說了列舉r1和r2，並使用雜湊表進行優化。

對於每個r1和r2，我們將c1固定為0，只列舉c2，並將(r1,0,r2,c2)的前綴和記做sm。一開始雜湊表都是空的，且空矩陣總和是0，故將0的計數初始化為1。 而target-sm記為diff，表示當前前綴和sm需要加上多少才能滿足target。所以回到雜湊表d中，查找總合為-diff的左方子矩陣有幾種可能，將d[-diff]更新到答案中，並將sm的計數+1。

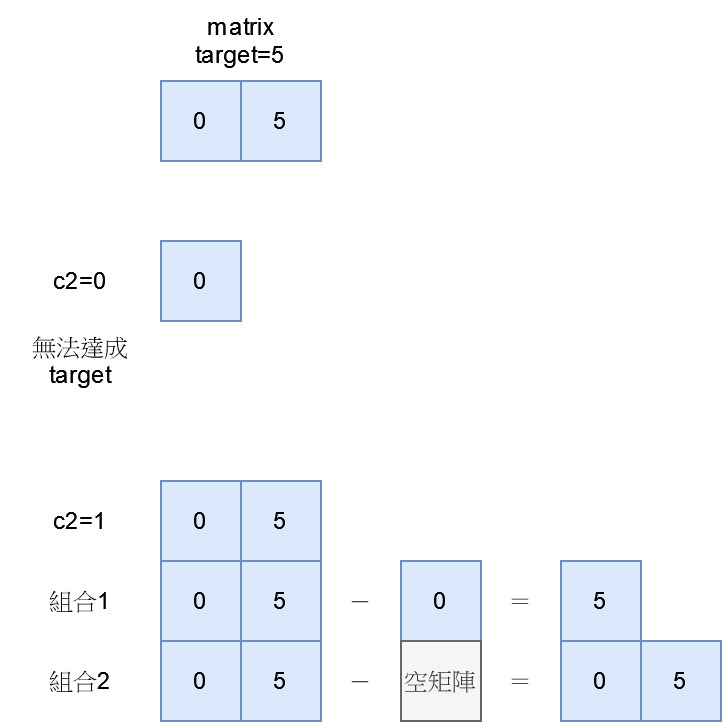
matrix=[[0,5]], target=5 c2=0，子矩陣[[0]]總和為0，不管怎樣都沒辦法滿足5
c2=1，子矩陣[[0,5]]總和為5，可以扣掉出現過的[[0]]或是空矩陣[[]]滿足target=5

class PrefixSum2D:
    def __init__(self, matrix):
        M, N = len(matrix), len(matrix[0])
        self.psum = [[0]*(N+1) for _ in range(M+1)]
        for r in range(M):
            for c in range(N):
                self.psum[r+1][c+1] = self.psum[r][c+1] + \
                    self.psum[r+1][c]-self.psum[r][c]+matrix[r][c]

    def rangeSum(self, r1, c1, r2, c2):
        return self.psum[r2+1][c2+1]-self.psum[r2+1][c1]-self.psum[r1][c2+1]+self.psum[r1][c1]
    
class Solution:
    def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
        M,N=len(matrix),len(matrix[0])
        ps=PrefixSum2D(matrix)
        ans=0
        for r1 in range(M):
            for r2 in range(r1,M):
                d=defaultdict(int)
                d[0]=1
                for c2 in range(N):
                    sm=ps.rangeSum(r1,0,r2,c2)
                    diff=target-sm
                    ans+=d[-diff]
                    d[sm]+=1
        return ans